Fórmula de Bhaskara

A Fórmula de Bhaskara é utilizada para encontrar as raízes de uma equação do segundo grau. O nome da fórmula é dada em homenagem ao matemático indiano Bhaskara Akaria, também conhecido por Bhaskara II.

No mundo acadêmico é comum dar o nome do pesquisador à sua obra. No Brasil, por volta de 1960, o nome de Bhaskara passou a designar a fórmula de resolução da equação do 2º grau. Não se vê essa nomenclatura em outros países, mesmo porque não foi ele quem a descobriu.

Historicamente existem registros de sua existência cerca de 4000 anos antes, em textos escritos pelos babilônios. Naquela época não existia a simbologia utilizada hoje, ou seja, não havia a fórmula atual, mas sim uma espécie de “receita” de como proceder para encontrar as raízes da equação quadrática. 

O método empregado por Bhaskara nas resoluções das equações quadráticas é do matemático indiano Sridhara (870-930 d.C.) e reconhecido pelo próprio Bhaskara. A fórmula para extrair essas raízes veio com um matemático francês, François Viète (1540-1603), que foi quem procurou dar um tratamento mais formal e algébrico para obter uma fórmula geral [1].

Atualmente as equações quadráticas são utilizadas em diversos problemas do dia a dia, tais como otimização, massa corpórea, nos movimentos uniformemente variados, cálculo de área, entre tantos outros.

Assim, a equação geral da equação do segundo grau é escrita da seguinte forma:

,

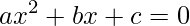na qual .  Então, para encontrar as raízes desta equação deve-se seguir os seguintes passos:

i) Calcular o valor do  :

.

ii) Calcular as raízes   e  :

          ;

          .

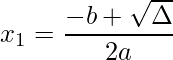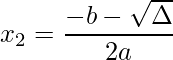A demonstração dessa solução da equação do segundo grau utiliza um método astucioso: o completamento de quadrados (inspirado, por sua vez, nos produtos notáveis) que permite simplificar a equação ao extrair a raiz quadrada ao eliminar o termo em   . Não vamos mostrar aqui, porque foge do nosso propósito de dar uma explicação mais objetiva da aplicação dessa fórmula. 

Exemplo: Encontre as raízes da equação 

Como ,  e  tem-se e :

          ;

          .

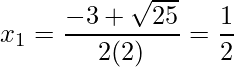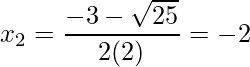Assim, as raízes da equação são 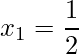   e  . Além disso, se quiser saber mais sobre o gráfico de funções quadráticas clique aqui. 

Portanto, esperamos que tenha ficado claro essa aplicação básica da Fórmula de Bhaskara.

Além disso, continuem nos acompanhando. Divulguem nosso site. Compartilhe esse post com os amigos e com aqueles que essa informação possa ser relevante. Se ficou alguma dúvida coloque nos comentários abaixo. Use seu login do Facebook. 

Referências

[1] UFRGS. «Bhaskara descobriu a fórmula de Bhaskara?». Consultado em 23 de julho de 2018.