Briot-Ruffini x Divisão Euclidiana 

Neste post apresentam-se duas formas de reduzir a ordem de um polinômio: o Algoritmo de Briot-Ruffini, criado por Paolo Ruffini, e a Divisão Euclidiana.

Quando tem-se um polinômio P(x) de ordem n, na qual $latex n\ge2&s=1$, é possível reescrevê-lo na forma de um produto de n polinômios de 1º grau, ou seja, da forma $latex x-a&s=1$. Então, um polinômio de 3º grau pode ser escrito na forma:

$latex P(x)=(x-a_{1})(x-a_{2})(x-a_{3})&s=1$ ,

onde os  $latex a_{n}&s=1$  representam as raízes do polinômio. Lembrando que estas raízes também podem ser números inteiros ou até mesmo complexos. Além disso, note que, se as raízes forem complexas, elas apareceram sempre em pares conjugados.

Redução da ordem de um polinômio por  Briot-Ruffini ou Divisão Euclidiana

Para aplicar o Algoritmo de Briot-Ruffini ou a Divisão Euclidiana, deve-se conhecer pelo menos uma das suas raízes. Então, sabendo que um polinômio P(x) de ordem n é a multiplicação dos n polinômios de 1ª ordem, sendo o termo independente de P(x)  representado pela multiplicação das n raízes de P(x), como no exemplo:

$latex P(x)=(x-a_{1})(x-a_{2})(x-a_{3})&s=1$ .

Assim, fazendo as multiplicações tem-se:

$latex P(x)=x^{3}-(a_{1}+a_{2}+a_{3})x^{2}+(a_{3}+1)(a_{1}+a_{2})x -a_{1}a_{2}a_{3}&s=1$ ,

onde  $latex a_{1}a_{2}a_{3}&s=1$  é o termo independente.

Portanto, as possíveis raízes do polinômio P(x) são os múltiplos do seu termo independente quando substituídos no próprio polinômio. Além disso, quando esse resultado é igual a 0, este número é uma raiz de P(x).

Algoritmo de Briot-Ruffini

O Algoritmo de Briot-Ruffini segue o seguinte esquema. Seja um polinômio $latex G(x)=c_{0}x^{n}+c_{1}x^{n-1}+\cdots+c_{n-1}x^{1}+c_{n}&s=1$  que possui raiz $latex a_{1}&s=1$ :

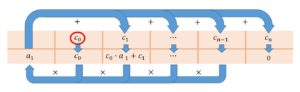
Percebe-se que na primeira linha deve-se colocar os coeficientes do polinômio G(x), em ordem decrescente segundo a potência do termo. A segunda linha inicia com a raiz conhecida e os demais são os novos coeficientes do polinômio reduzido Q(x). Além disso,  lembrando que o último elemento deve ser sempre 0, pois possui um termo a menos que o polinômio original.

Então, o algoritmo para encontrar o polinômio Q(x) segue os seguintes passos, para cada novo coeficiente:

1º) Copiar 1º coeficiente do polinômio G(x) (em destaque);

2º) Multiplicar o 1º coeficiente de Q(x) pela raiz  $latex a_{1}&s=1$  e somar com o 2º coeficiente de G(x);

3º) Multiplicar o 2º coeficiente de Q(x) pela raiz  $latex a_{1}&s=1$ e somar com o 3º coeficiente de G(x).

Assim, deve-se fazer este mecanismo até chegar na última coluna e verificar que o resultado dê 0.

Divisão Euclidiana

A divisão Euclidiana de polinômios é similar a divisão de dois números quaisquer, na qual tem-se um polinômio G(x) chamado dividendo e outro D(x) chamado divisor,  que em nosso caso é do 1º grau que contém a raiz conhecida. Ao dividir G(x) por D(x) obtém-se um polinômio Q(x), chamado de quociente, e outro R(x) chamado de resto, que em nosso caso é sempre 0. Na figura apresenta-se um esboço desta divisão:

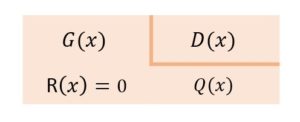
Portanto, pode-se obter o mesmo polinômio Q(x), mas na nossa opinião, um pouco mais trabalhosa que pelo  algoritmo de Briot-Ruffini.

Além disso, no post seguinte apresenta-se um exemplo numérico do algoritmo de Briot-Ruffini e Divisão Euclidiana.