Domínio e Imagem de uma Função Racional
Vamos calcular o Domínio e Imagem de uma Função Racional, sabendo que ![]() e
e
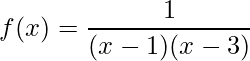 .
.
Para resolver o domínio de uma função que contém a variável independente ![]() no denominador de uma fração deve-se perguntar:
no denominador de uma fração deve-se perguntar:
Para quais valores
a fração está definida?
Ou, novamente, pode-se fazer a pergunta inversa:
Existe algum valor de
em que torna a fração indefinida?
Para encontrar o Domínio de uma Função Racional, a forma mais fácil é analisar a segunda pergunta, pois sabe-se que não existe divisão por 0. Então, basta observar o denominador e encontrar os valores de ![]() que o torna 0.
que o torna 0.
Neste nosso exemplo, tem-se dois casos:
1º) ![]() ;
;
2º) ![]() .
.
Facilmente pode-se resolver essas equações e obter ![]() e
e ![]() . Assim, o domínio pode ser escrito da seguinte forma:
. Assim, o domínio pode ser escrito da seguinte forma:![]() , ou ainda:
, ou ainda:
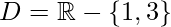 .
.
Além disso, o passo seguinte é calcular a imagem nessa função. A forma mais simples de calcularmos a imagem de uma função é através da interpretação gráfica, na qual deve-se construir o esboço do gráfico da função ou através de um software, como o GeoGebra. Em seguida, observa-se para quais valores de ![]() tem-se valores de
tem-se valores de ![]() correspondente.
correspondente.
Para construir o esboço do gráfico deve-se observar as seguintes informações:
1) Assíntotas verticais em ![]() e
e ![]() (retas verticais que não interceptam o gráfico da função);
(retas verticais que não interceptam o gráfico da função);
2) Comportamento do gráfico nos extremos (![]() e
e ![]() );
);
3) Comportamento do gráfico quando se aproxima das assíntotas verticais;
4) Pontos de máximo ou de mínimo.
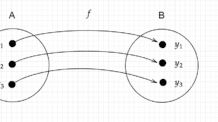
Portanto, fazendo estas análises obtém-se o seguinte esboço:

Assim, é possível perceber que a imagem da função dada é:
![]() .
.
Caso desejar, confira a resolução do Domínio e Imagem de uma Função Racional em vídeo: Clique aqui.
Portanto, esperamos que tenha ficado claro esse post sobre Domínio e Imagem de uma Função Racional.
Além disso, continuem nos acompanhando. Divulguem nosso site. Compartilhe esse post com amigos e com aqueles que essa informação possa ser relevante. Se ficou alguma dúvida, coloque nos comentários abaixo. Use seu login do Facebook.


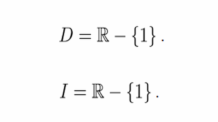

Deixe um comentário