Domínio e Imagem de uma Função Racional

Neste post vamos encontrar o Domínio e Imagem de uma Função Racional sabendo que e

.

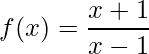Domínio da função 

Neste exemplo tem-se uma função racional, ou se preferir, uma função fracionaria, na qual possui razão entre polinômios de primeira ordem. Para encontrar o domínio desta função usa-se a mesma metodologia usada no Exemplo 2.  Então, ao observar a fração, deve-se perguntar:

Quais são os valores de que torna o denominador nulo?
O polinômio do numerador possui alguma restrição?  

Denominador: percebe-se que a variável independente não pode assumir o valor 1, uma vez que nesse valor o denominador torna-se nulo.

Numerador: o polinômio do numerador não possui nenhuma restrição.

Portanto, o domínio dessa função são todos os reais menos o 1, simbolicamente escreve-se:

    .

Imagem da função 

Após determinar o domínio da função, deve-se encontrar a imagem correspondente a este domínio. Da mesma forma, como nos exemplos anteriores, sugere-se determinar a imagem a partir da interpretação gráfica da função. Por isso, propomos construir um esboço do gráfico ou se você preferir utilize um software matemático como o GeoGebra.

Para construir o esboço deve-se analisar:

1) O comportamento da função nos extremos ( e ).
Aqui nota-se que nos extremos tem-se uma divisão de dois números quase iguais e muito grandes. Logo, quanto maior for o valor de , tanto para valores positivos como para negativos, tem-se o valor de  cada vez mais próximo de 1.

2) O comportamento da função próximo da assintota vertical,  pela direita.
Aqui tem-se uma divisão de um numerador muito próximo de 2 e um denominador negativo muito pequeno. Logo, quanto mais próximo de 1 estivermos, o resultado da divisão tende a .

3) O comportamento da função próximo da assintota vertical,  pela esquerda.
Aqui tem-se uma divisão de um numerador muito próximo de 2 e um denominador positivo muito pequeno. Logo, quanto mais próximo de 1 estivermos, o resultado da divisão tende a .

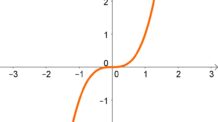
Assim, pode-se construir o esboço da função: 

Além disso, ao observar o esboço do gráfico percebe-se que o mesmo assume todos os valores de , exceto , que é uma assíntota horizontal, logo a imagem é:

    .

Caso desejar,  confira também a resolução do Domínio e Imagem de uma Função Racional em vídeo: Clique aqui. 

Portanto, esperamos que tenha ficado claro esse post sobre Domínio e Imagem de uma Função Racional. Continuem nos acompanhando. Divulguem nosso site. Compartilhe esse post com amigos e com pessoas que essa informação possa ser relevante. Além disso, se ficou alguma dúvida coloque nos comentários abaixo. Use seu login do Facebook.