Gráfico das Funções Básicas

As funções básicas são um grupo de funções que são originais e que servem de base para a construção das outras funções. Então, fazer o Gráfico das Funções Básicas é representar a função no plano cartesiano, na qual sua aparência é uma curva. Esta curva é formada por todos os pontos que descrevem a função. Além disso, no caso de uma função que tenha a variável independente e a variável dependente , em que no plano cartesiano, os pontos do gráfico são formados pelo par ordenado .

Muitas vezes, no estudo das funções não há a necessidade de gráficos completos, com todos os detalhes. Precisamos apenas de uma ideia geral do comportamento da função e alguns pontos importantes por onde ela passa. Esta figura chama-se esboço da função.

A seguir apresentam-se algumas dicas de como construir os esboços das funções básicas. 

• Função Constante 

  São aquelas que independem da variável 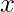, na qual para todo o domínio ela permanece com o mesmo valor. Por exemplo, :

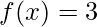• Função Potência  

  São aquelas funções em que a variável independente 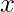está elevada à uma potência. Quando for um número natural, o grau da potência representa a quantidade de raízes que a função possui, sendo que algumas das raízes podem não ser reais. As demais são os pontos onde interceptam o eixo 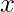, exemplos: 

Além do mais, dentro das funções potência existe o caso particular em que a potência é fracionária, por isso este tipo de função é chamada de Função Raiz, uma vez que . Veja dois exemplos e repare no domínio: 

• Função Racional  

  São as que possuem a variável independente no denominador de uma fração. Como o denominador de uma fração deve ser diferente de 0, no domínio aparecem algumas restrições. Assim, nestes pontos não haverá gráfico, na qual chama-se de Assíntotas Verticais.  Exemplo:

Neste exemplo, nota-se também uma Assintota Horizontal. 

• Função Exponencial 

  É quando tem-se a variável independente no expoente e uma constante na base. Talvez a função exponencial mais conhecida e utilizada seja a que contém na base o número de Euler, ou seja, o famoso :

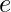• Função Logarítmica

  É a função  que possui a variável independente no logaritmando, sendo que a base deve ser positiva e diferente de 1. Note que, o domínio desta função são todos os reais positivos. Além disso,  lembre-se que 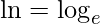, exemplo:    

• Funções  Trigonométricas

  São funções angulares na qual estão relacionadas com o arco trigonométrico. Lembrando que as funções assumem o mesmo comportamento periódico, exemplos:

Além do mais, complemente seu estudo de Funções Trigonométricas com o post das Relações Trigonométricas.  Além disso, se quiser saber mais sobre o gráfico de funções trigonométricas clique aqui. 

Caso você preferir, construa o Gráfico das Funções Básicas em um software como o Geogebra.