Gráfico de Funções: Combinando Funções
O Gráfico de Funções: Combinando Funções gera uma infinidade de novas funções a partir das Funções Básicas. Por isso, a grande maioria das funções são combinações de pelo menos outras duas. Um exemplo muito comum são as funções polinomiais, na qual são combinações de funções potência.
Sejam as funções ![]() e
e ![]() . Então, pode-se construir novas funções utilizando os seguintes operadores:
. Então, pode-se construir novas funções utilizando os seguintes operadores:
1) Soma: ![]() ;
;
2) Subtração: ![]() ou
ou ![]() ;
;
3) Multiplicação: ![]() ;
;
4) Divisão: ![]() ou
ou ![]() ;
;
5) Composição: ![]() ou
ou ![]() ;
;
Obs: Como as operações da soma e da multiplicação independem da posição, por isso é apresentado apenas uma delas.
Construindo alguns exemplos
Considerando as funções ![]() e
e 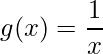 , encontre:
, encontre:
1) 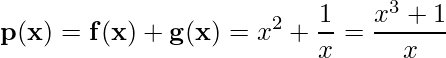 ;
;
2) 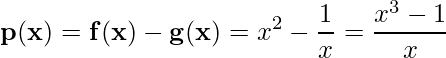 ;
;
3) 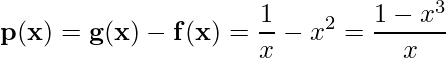 ;
;
4) 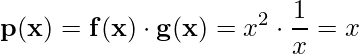 ;
;
5) 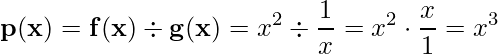 ;
;
6) 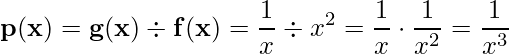 ;
;
7) 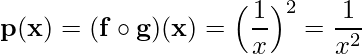 ;
;
8) 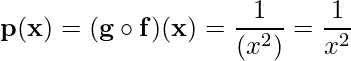 ;
;
Além disso, ao construir uma nova função a partir da combinação de outras, a nova recebe uma combinação das características da função original. Ou seja, seu domínio, imagem e o comportamento gráfico serão uma combinação de outras funções . Por exemplo, as funções apresentadas no item 1.
Domínio das funções:
![]() é
é ![]() ;
;
![]() é
é ![]() ;
;
![]() é
é ![]() .
.
Imagem das funções:
![]() é
é ![]() ;
;
![]() é
é ![]() ;
;
![]() é
é ![]() .
.
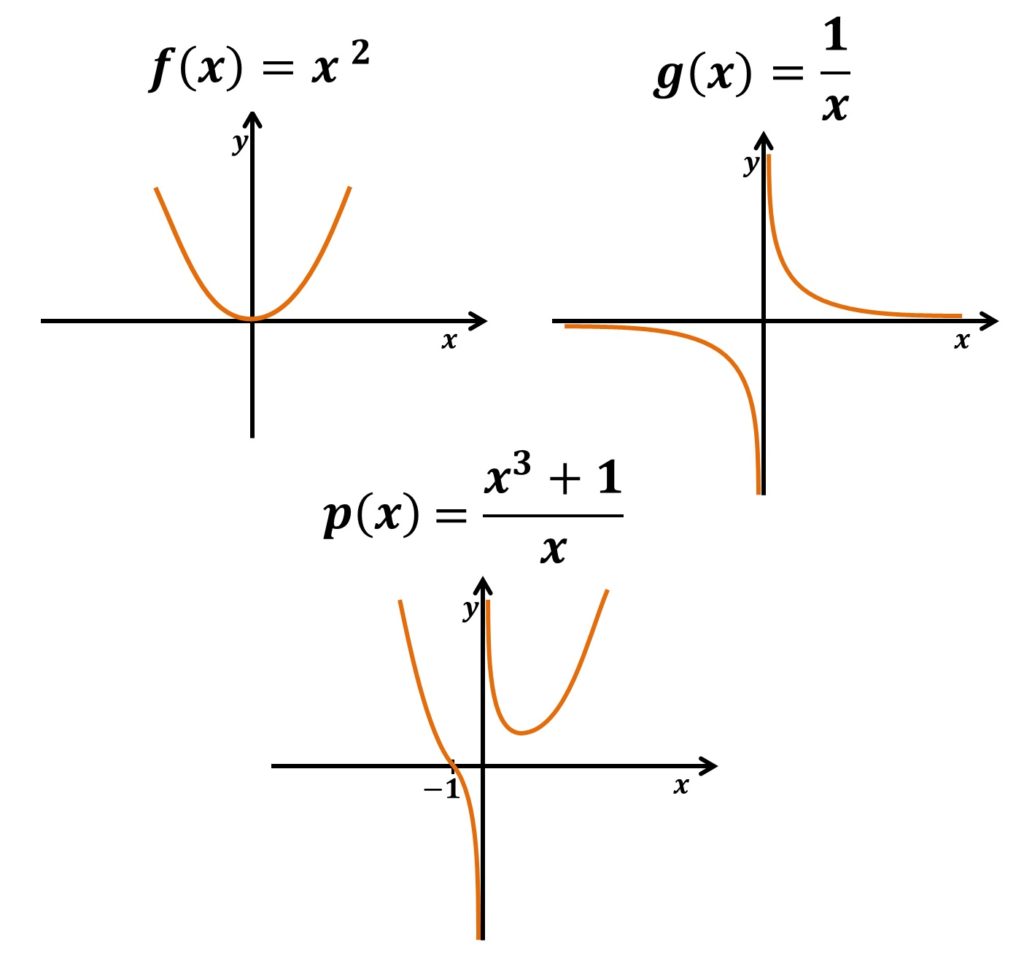
Assim, ao observar o gráfico da nova função, percebe-se facilmente as características das funções originantes. Logo, nos extremos, o comportamento da ![]() predomina e no entorno de zero predomina a função
predomina e no entorno de zero predomina a função ![]() , uma vez que a
, uma vez que a ![]() tende a zero.
tende a zero.
Além disso, caso queira ver outra combinação de um Gráfico de Funções: Combinando Funções, clique aqui.
Portanto, esperamos que tenha ficado claro esse post sobre Gráfico de Funções: Combinando Funções.
Além do mais, continuem nos acompanhando. Divulguem nosso site. Compartilhe esse post com amigos e com aqueles que essa informação possa ser relevante. Por fim, se ficou alguma dúvida, coloque nos comentários abaixo. Use seu login do Facebook.



Deixe um comentário