Gráfico de Funções: Alongamentos e Compressões

O Gráfico de Funções: Alongamentos e Compressões consiste em multiplicar por uma constante  toda a função, , ou apenas o argumento da função, , alterando assim a imagem da função.

Considerando que a constante seja positiva. Para não confundir com o efeito da reflexão, opta-se por trabalhar apenas com valores maiores do que 0.

Constante multiplicando a função

Quando uma função é multiplicada por uma constante da seguinte forma, , altera-se o valor da imagem () proporcionalmente ao fator multiplicado. Logo, tem-se dois casos distintos:

1º Caso: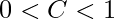   

Neste caso, tem-se uma compressão do gráfico da função. Por isso, quando comparado com o gráfico original, este novo fica menor (mais achatado), na direção vertical.

Assim, veja o que acontece com a função :

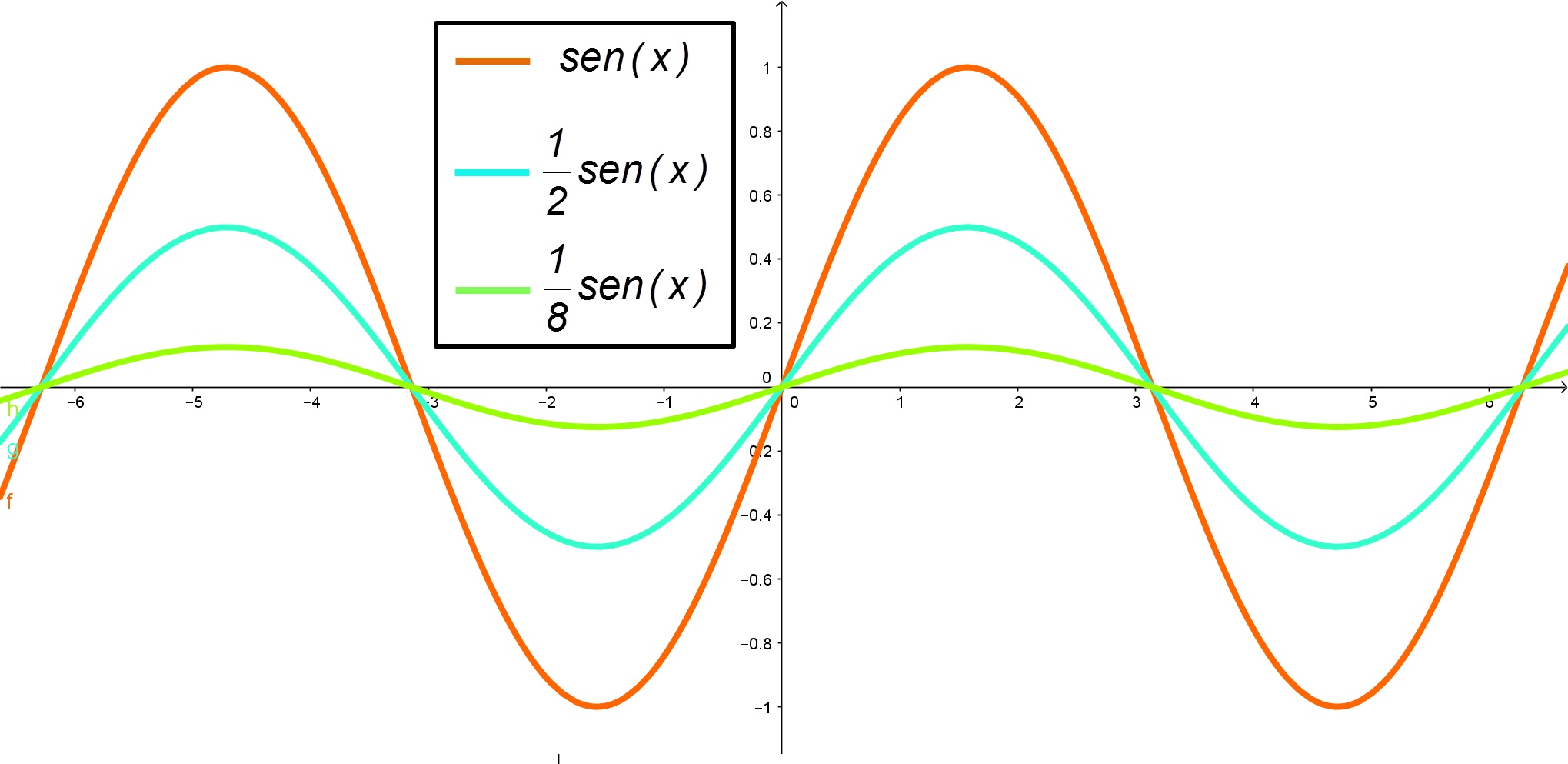
2º Caso: 

Neste outro caso, tem-se um alongamento do gráfico da função. Por isso, quando comparado com o gráfico original, este novo fica maior (mais alongado), na direção vertical. 

Assim, veja o que acontece com a função :

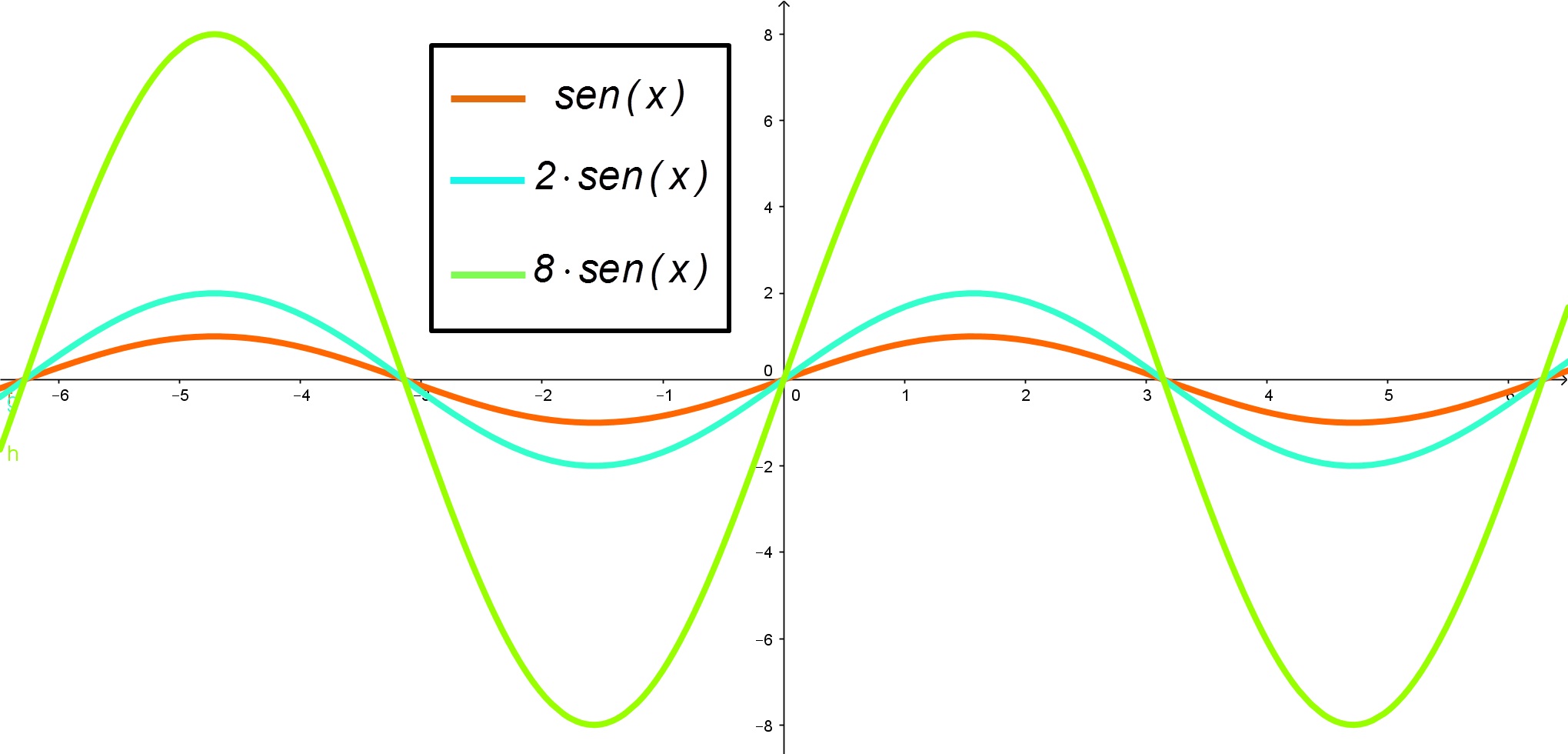
Obs: ao multiplicar uma função trigonométrica por uma constante altera-se a amplitude desta função. 

Constante multiplicando o argumento de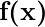

1º Caso: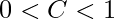 

Neste caso, tem-se um alongamento do gráfico da função. Por isso, quando comparado com o gráfico original, este novo fica maior (mais alongado), na direção horizontal. 

Assim, veja o que acontece com a função  :

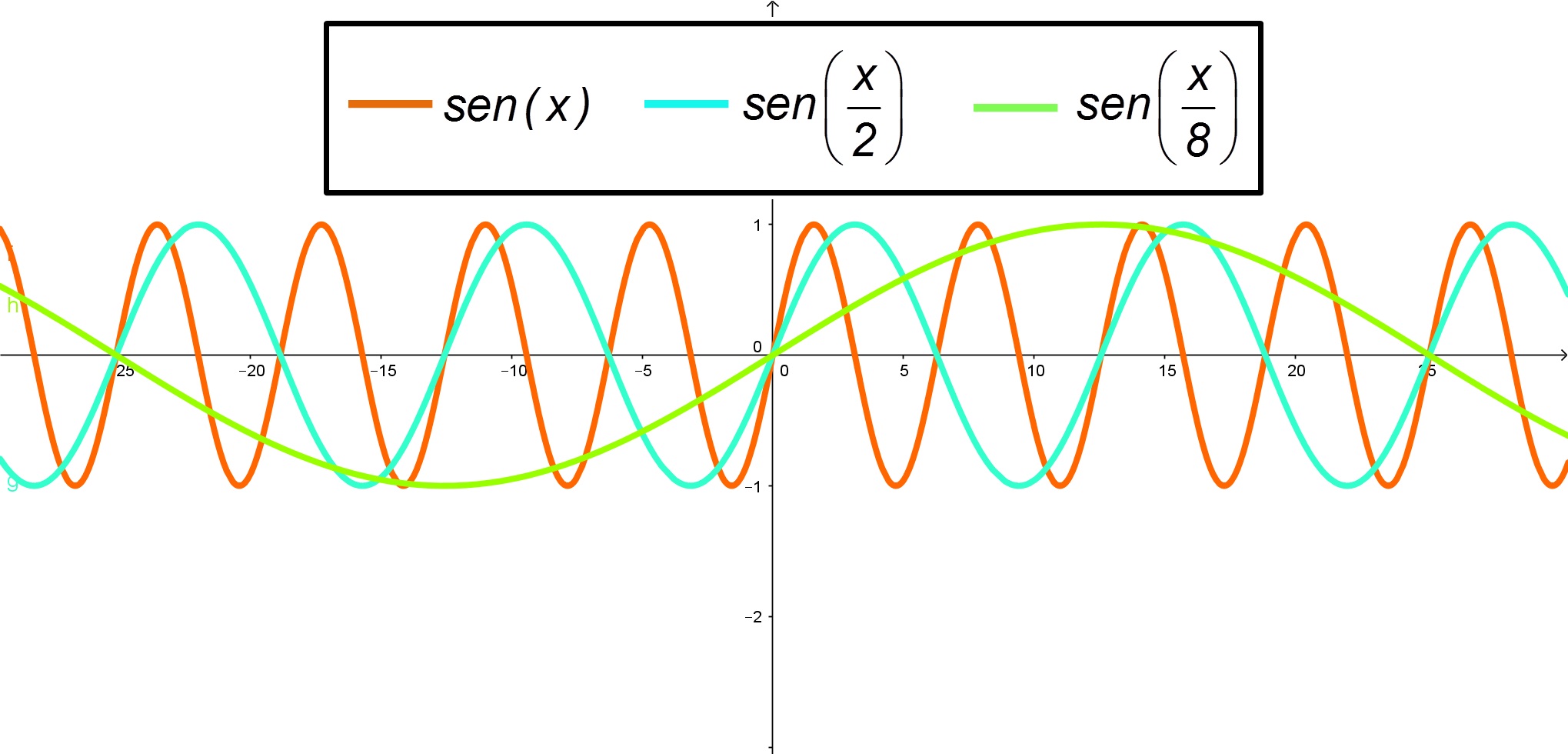
2º Caso: 

Neste caso, tem-se uma compressão do gráfico da função, ou seja, quando comparado com o gráfico original.  Por isso, este novo fica menor (mais achatado), na direção horizontal.

Assim, veja o que acontece com a função  :

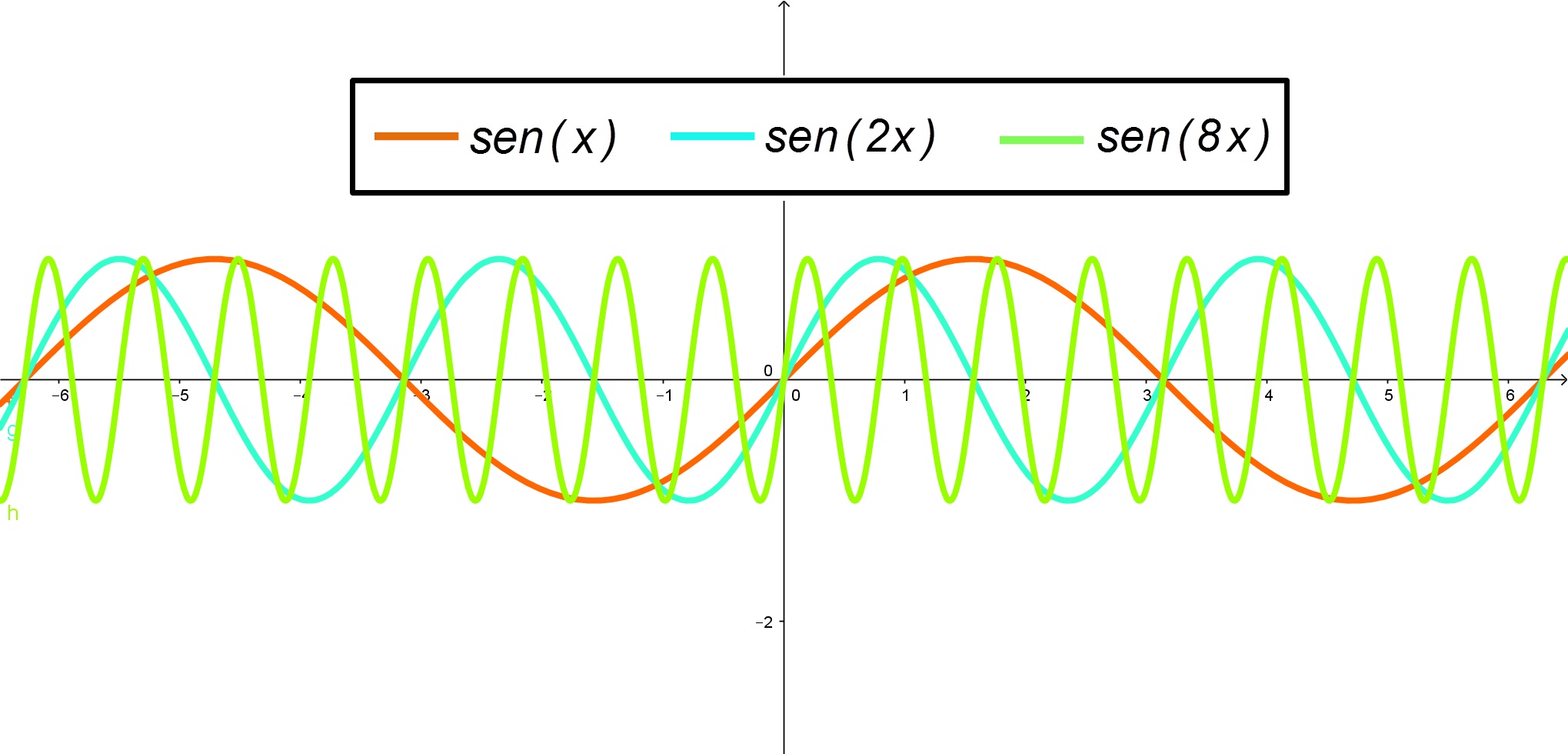
Obs: ao multiplicar uma constante no argumento de uma função trigonométrica altera-se a frequência desta função. 

Além do mais, assista também em vídeo: Alongamentos e Compressões Parte 1 e Alongamentos e Compressões Parte 2. 

Portanto, espero que tenham gostado desse post sobre Gráfico de Funções: Alongamentos e Compressões. Continuem nos acompanhando. Divulguem nosso site. Compartilhem esse post com os amigos e para quem essa informação possa ser relevante. Se ficou alguma dúvida coloque nos comentários abaixo. Use seu login do Facebook.