Número Pi: razão entre o perímetro e o diâmetro de uma circunferência

Desde a antiguidade percebeu-se que a divisão do perímetro pelo diâmetro de qualquer circunferência resultava sempre no mesmo número, o Número Pi.

No século III a.C, Arquimedes já estimava que este número estaria entre 3,1408 e 3,1428. Ao longo dos anos, percebeu-se que não teria como expressar este número com exatidão, pois ele é irracional.

A primeira utilização do símbolo  para representar pi deve-se a William Jones em 1706, sendo depois adotada por Euler em 1748. Logo, se popularizou e tornou a notação padrão para esta constante.

Pode-se provar que o número  é irracional e transcendente.

Um número diz-se irracional quando não pode ser representado por uma fração de dois inteiros e transcendente se não anular nenhuma função polinomial de coeficientes inteiros.

Assim, no século XVIII foi adotada a letra grega como sendo a razão entre o perímetro e o diâmetro de qualquer circunferência.

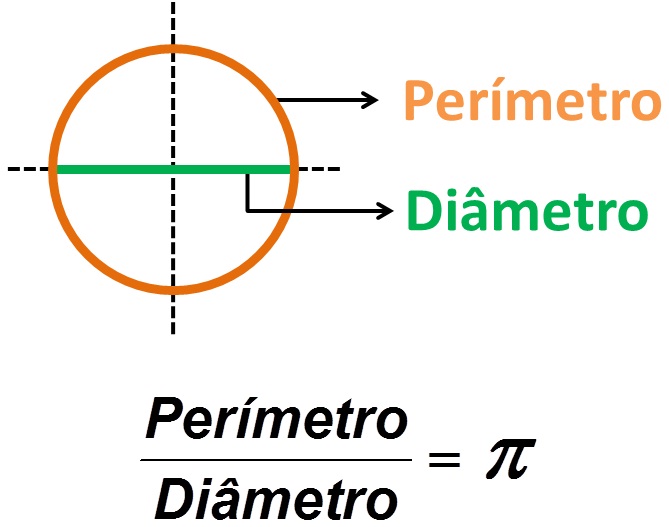
Entretanto, dependendo da precisão necessária nos cálculos, adotam-se diferente valores de aproximação. Em exercícios escolares utiliza-se normalmente 3,14 ou no máximo 3,1416.

Já em cálculos mais precisos, como na exploração do espaço, segundo o engenheiro-chefe da missão Dawn da NASA, Marc Rayman, relata terem usado 3,141592653589793.

Além disso, baseado no método de Arquimedes é possível formular uma representação matemática para o cálculo de pi. Essa forma é eficiente para um polígono de qualquer número de lados.

Considerando um polígono de n lados e raio 1, temos a medida do lado expressa pela lei dos cossenos:

Temos formado um triângulo isósceles, de base l e lados r=1:

O ângulo do triângulo isósceles no centro do polígono é expresso por 360º dividido pelo número de lados (n), portanto:

Dessa forma, o perímetro do polígono será de:

Como  é representado pelo perímetro do polígono dividido pelo seu diâmetro, temos:

Aplicando transformações trigonométricas, a fórmula acima pode ser simplificada para: