Funções Trigonométricas Inversas

Neste post vamos falar um pouco sobre as Funções Trigonométricas Inversas.

Dentro da matemática quase todas as operações possuem suas respectivas operações inversas, como por exemplo:

1) Soma  → subtração;

2) Multiplicação → divisão;

3) Potenciação → radiciação;

4) Exponencial → logarítmica.

E não é diferente com as funções trigonométricas, na qual tem-se as suas respectivas funções inversas.  

As Funções Trigonométricas Inversas são muito importantes nos cálculos, pois muitas vezes queremos saber qual é o ângulo que originou determinado valor. Por exemplo:

.

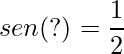Assim, sabendo qual é a função inversa de seno, obtém-se o valor do ângulo desejado. Agora tomem cuidado!!! O valor do ângulo deve ser em radianos. (Para converter para graus basta fazer uma regra de três: ) .

Simbolicamente, as Funções Trigonométricas Inversas podem ser escritas de duas formas, por exemplo: 

  ou   , 

  ou   , 

   ou    . 

Cuidado: 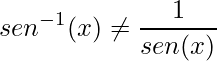. Análogo para todas as funções trigonométricas.

Gráfico das Funções Trigonométricas Inversas

Primeiramente, deve-se lembrar que para existir uma função inversa , a função  deve ser injetora. Ou seja, para cada tem-se um único e para cada um único . Então, para ser mais preciso, a função deve ser bijetora (injetora + sobrejetora). Como, de uma forma geral, admite-se que a imagem é igual ao contradomínio (sobrejetora), basta a função ser injetora. 

Além do mais, como as Funções Trigonométricas são periódicas, ou seja, o comportamento se repete a cada determinado período, elas não atendem ao critério da bijeção.

Assim, o gráfico das Funções Trigonométricas Inversas deve ser restrito a uma parte do domínio de  .

Obs: O gráfico das Trigonométricas Inversas é simétrico em relação a reta  ao gráfico das suas funções trigonométricas correspondentes, conforme gráficos a seguir:

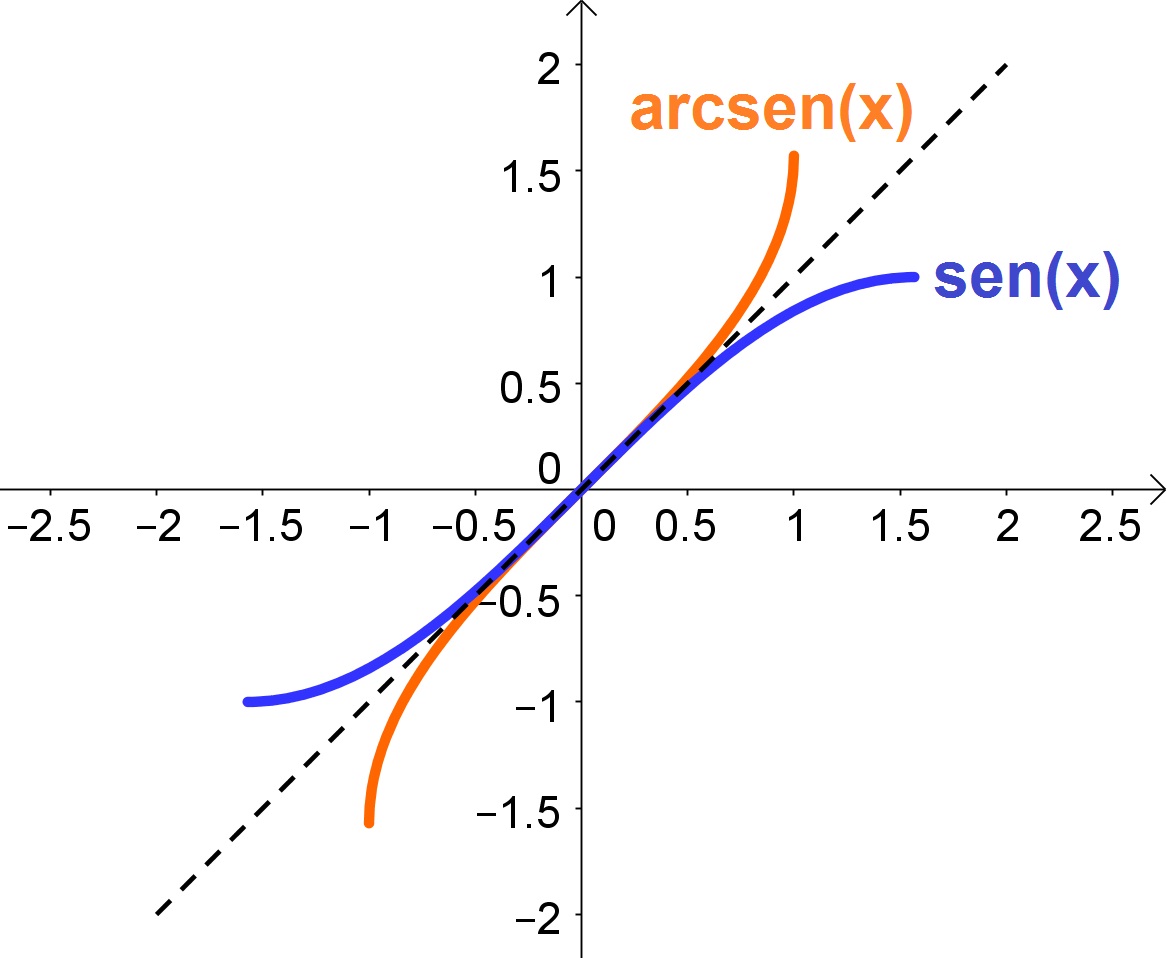
Veja mais detalhes da construção do gráfico da função Arco Seno em vídeo, clicando aqui.

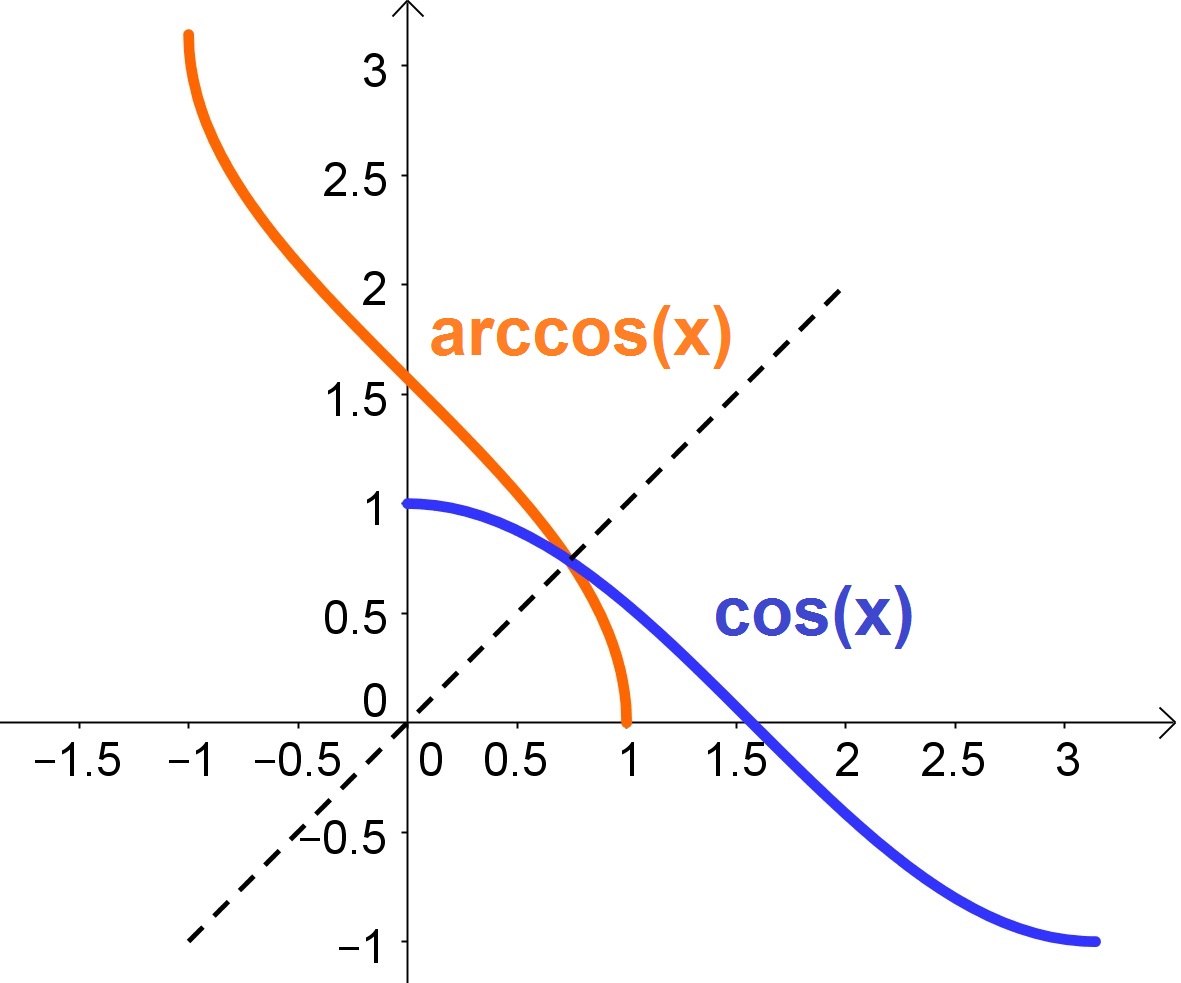
Veja mais detalhes da construção do gráfico da função Arco Cosseno em vídeo, clicando aqui. 

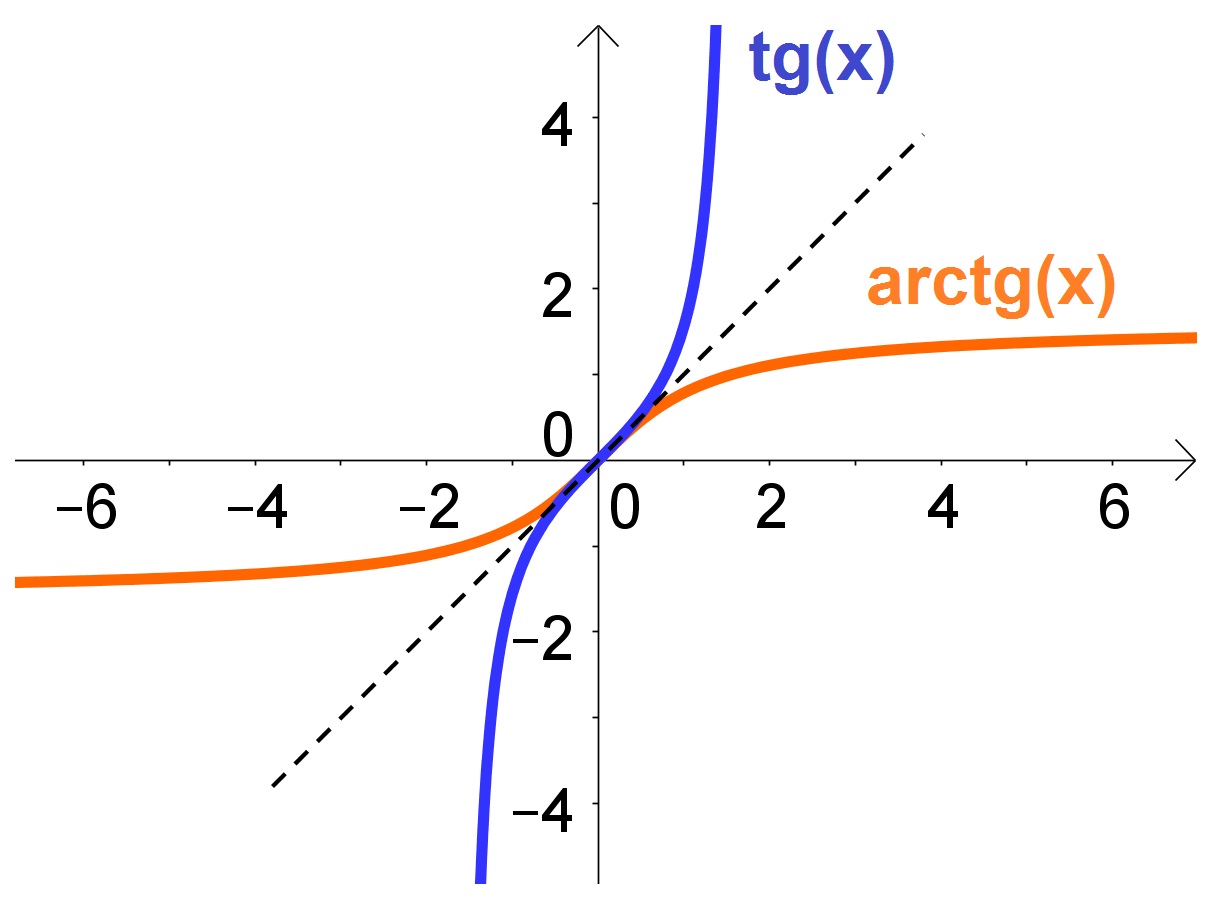
Veja mais detalhes da construção do gráfico da função Arco Tangente em vídeo, clicando aqui. 

Portanto, espero que tenha ficado claro esse post sobre Funções Trigonométricas Inversas. Continuem nos acompanhando. Divulguem nosso site. Compartilhem esse post com amigos e com aqueles que isso posso ser importante. Além disso, se ficou alguma dúvida deixe nos comentários abaixo usando seu login do Facebook. 

Grande abraço.