Gráfico das Funções Trigonométricas

Construir o Gráfico das Funções Trigonométricas é representar no plano cartesiano as funções trigonométricas, onde a variável  representa o valor do ângulo em radianos e em  o correspondente valor da função.

Uma das principais características deste tipo de função é a periodicidade. A cada determinado comprimento (período) os valores da função se repete. Então, pode-se escrever simbolicamente da seguinte forma:

,

onde  é o período.

Caso você ainda não tenha domínio sobre os conteúdos das relações trigonométricas dê uma parada e retome isso, pois é essencial para construir o gráfico das funções trigonométricas.

Assim, iniciamos abordando as funções trigonométricas básicas do e do , na qual são bases das demais funções e que já foram construídas no post das Funções Básicas. 

Além das características já citadas, estas duas funções são continuas e limitadas, ou seja, elas se encontram dentro de uma faixa de valores em  .

Além disso, esta faixa de valores está relacionada a constante que acompanha estas duas funções. No caso das funções originais ( e ) vão de  a   .

Caso a contante que as acompanha for, por exemplo, tem-se . Deste modo, a faixa de valores em é de  a   .  

Os demais gráficos das funções trigonométricas são feitos a partir destas duas funções. Por exemplo, o gráfico da função tangente, em que a função pode ser escrita da seguinte forma: 

.

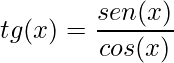Além do mais, quando deseja-se traçar o gráfico de uma função que contenha a variável independente no denominador, deve-se tomar o cuidado de analisar em quais pontos ela não é definida, visto que o denominador não pode ser igual a 0.

Na função em questão deve-se perguntar:

Para quais valores ?

Aqui percebe-se que são todos os valores escritos da seguinte forma: 

,

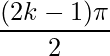onde são os números inteiros.  Nestes pontos o domínio não está definido e tem-se assíntotas verticais.

O próximo passo para construir o gráfico é analisar o comportamento da função próximo destas assíntotas, onde percebe-se que à esquerda das assíntotas o gráfico vai a mais infinito e à direita menos infinito.    

Por fim, deve-se analisar quais são as raízes da função , ou seja, onde . Neste caso são os pontos onde  .

Gráfico

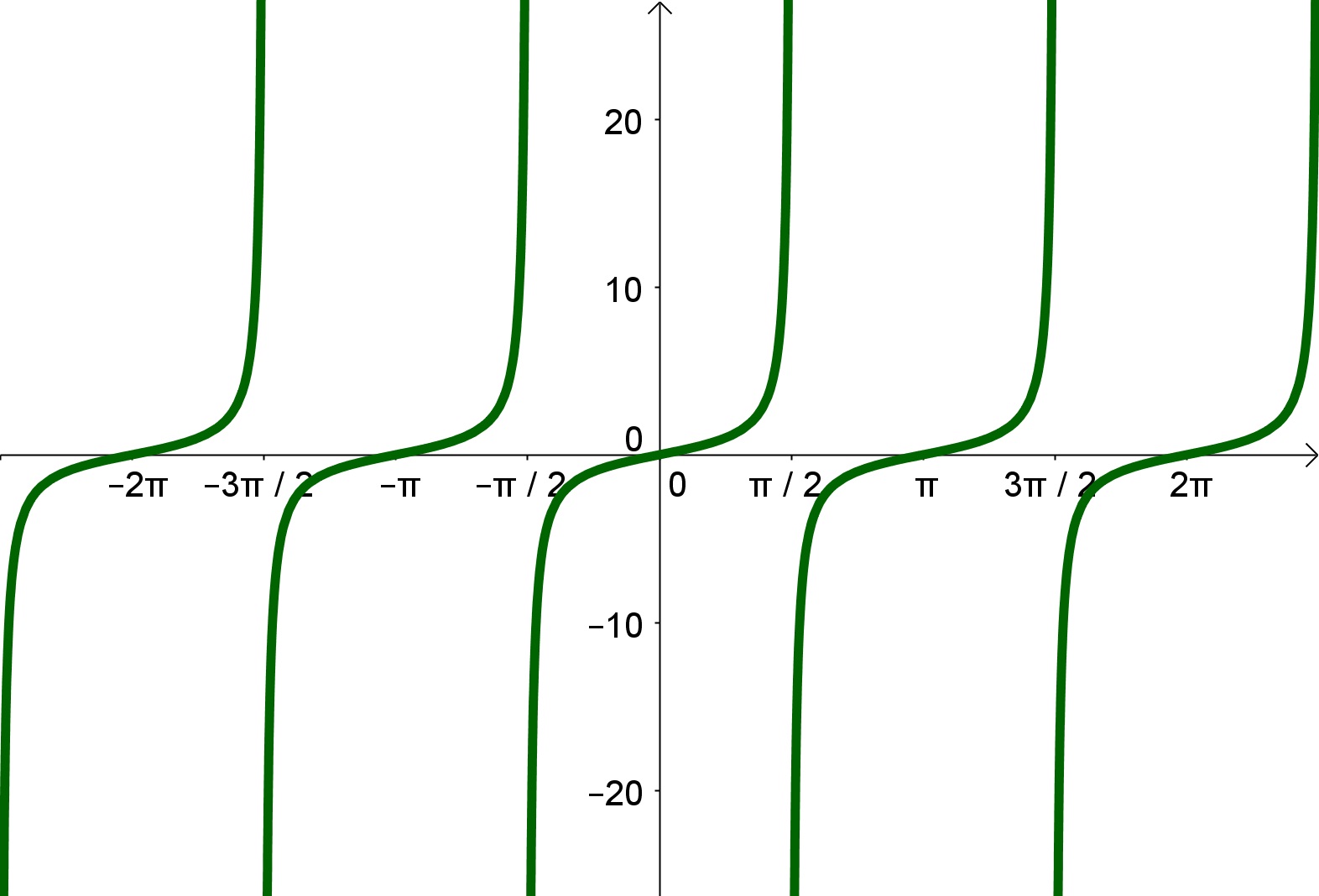
Para as demais funções trigonométricas o processo da construção do gráfico é de forma análoga.  Veja um exemplo em vídeo clicando aqui.