Limite: Definição Formal

Neste post, vamos começar com Limite: Definição Formal.

Cabe ressaltar que, em matemática, o conceito de limite é usado para descrever o comportamento de uma função à medida que o seu argumento se aproxima de um determinado valor. Assim como o comportamento de uma sequência de números reais, à medida que o índice (da sequência) vai crescendo, i.e. tende para infinito. Os limites são usados no cálculo diferencial e em outros ramos da análise matemática para definir derivadas e a continuidade de funções.

Seja um intervalo qualquer,  e  uma função definida no intervalo , (exceto eventualmente em ). Diz-se que o limite de  quando tende a é .   Escreve-se , se para todo existe um , tal que

 sempre que   ,

onde  e são constantes tão pequenas quanto se queira.

Em outras palavras, pode-se dizer que uma função possui limite em  se os pontos em x presentes em um pequeno intervalo entorno de  produzem valores de  em um pequeno intervalo entorno de  .

Gráfico

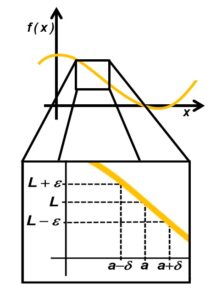
A noção de limite é fundamental no início do estudo de cálculo diferencial. O conceito de limite pode ser aprendido de forma intuitiva, pelo menos parcialmente.

Quando falamos do processo limite, falamos de uma incógnita que “tende” a ser um determinado número. Ou seja, no limite, esta incógnita nunca vai ser o número. Entretanto, vai se aproximar muito, de tal maneira que não se consiga estabelecer uma distância que vai separar o número da incógnita. Em poucas palavras, um limite é um número para o qual y = f(x) difere arbitrariamente muito pouco quando o valor de x difere de x₀ arbitrariamente muito pouco também. 

Então, no limite é como se pudéssemos substituir o valor de x para resolvermos o problema. Na verdade, não estamos substituindo o valor. Porque para o cálculo não importa o que acontece no ponto x, mas sim o que acontece em torno deste ponto. Por isso, quando falamos que um número “tende” a ser n, por exemplo, o número nunca vai ser n, mas se aproxima muito do número n. Enfim, como foi dito anteriormente, a definição de limite é tão e somente intuitiva. Vai de analisar a função que está ocorrendo apenas. 

Portanto, esperamos que tenha entendido o post Limite: Definição Formal. Continue nos acompanhando. Divulguem nosso site. Compartilhe esse post. Se ficou alguma dúvida coloque nos comentários abaixo. Use seu login do Facebook. 

De sequência nos seus estudos com o tópico Propriedades dos Limites. Além do mais, prossiga seus estudos assistindo esse vídeo.