Indeterminação no cálculo dos Limites

A Indeterminação no cálculo dos Limites ocorre quando calcula-se o limite de uma função e nos deparamos com os seguintes símbolos:

Veja um exemplo onde isto ocorre:

.

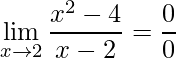Logo, nestes casos tem-se que repensar o procedimento de cálculo fazendo alguma manipulação algébrica na expressão para superar esta indeterminação.  

Assim, apresentam-se neste post três formas de contornar essa indeterminação:

• Fazendo fatoração, utilizando o Algoritmo de Briot-Rufini.

Exemplo:

.

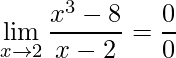Aplicando Briot-Rufini no numerador obtém-se: 

.

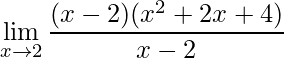Simplificando o termo em comum tem-se: 

.

• Racionalizando 

Este método é utilizado quando no numerador ou denominador contém uma raiz, por isso a estratégia é racionalizar o termo que contém a raiz.

Exemplo:

.

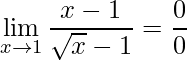Assim, deve-se multiplicar tanto o numerador quanto o denominador pelo termo que contem a raiz, porém com sinal contrário: 

.

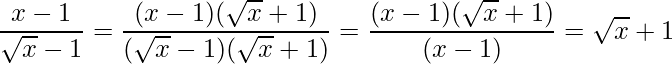Logo, tem-se:

.

• Fazendo mudança de variável

Este método considera-se como sendo um truque algébrico em que se utiliza para facilitar a solução da indeterminação. Observe através de um exemplo: 

.

Note que, para contornar isso faz-se uma mudança de variável do tipo  . Assim, elevando ao cubo nos dois lados tem-se que: , logo .

Além disso, deve-se também transformar o ponto ao qual se quer saber o limite. A partir da equação  podemos dizer que, quando também .

Assim, substituindo tem-se: 

.

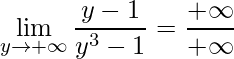Além do mais, notem que aqui ainda temos uma indeterminação, por isso reescrevendo o denominador utilizando Briot-Rufini fica-se com:  

.

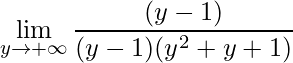Por conseguinte, simplificando e resolvendo tem-se:

.

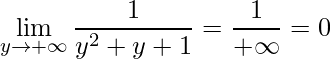Outra estratégia seria dividir o numerador e o denominador por , na qual fica-se com: 

.

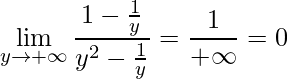Cabe ressaltar que, outra forma de superar as indeterminações do tipo  ou  é utilizando a Regra de l’Hôpital. No entanto, necessita-se ter o conhecimento de derivadas. Por isso, apresentaremos essa regra após postar o conteúdo sobre derivadas.

Portanto, espero que tenham gostado do Post Indeterminação no cálculo dos Limites. Continuem nos acompanhando. Compartilhem esse Post com os amigos. Divulguem nosso site.  Se ficou algum dúvida, escreva nos comentários abaixo usando seu login do Facebook.

Continue seus estudos fazendo uma prova online de limites, ou ainda, acompanhe outros exemplos clicando aqui ou assista outra explicação em vídeo aqui.