Limites Fundamentais

Neste post apresentam-se os Limites Fundamentais e suas demostrações, porque eles aparecem com frequência na resolução dos exercícios.

1º Limite Fundamental

$\displaystyle \lim\limits_{x\rightarrow 0}\frac{sen(x)}{x}=1$ .

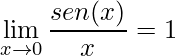Para demostrar este limite utiliza-se a figura abaixo, na qual contém um setor circular de raio 1 e dois triângulos com um dos seus ângulos internos medindo $\displaystyle 0<x<\frac{\pi}{2}$ (em radianos).

Facilmente percebe-se que:

$\overline{AC}\leq B\hat{O}C\leq \overline{BD}$ .

Abstraindo:

1) Considerando o triângulo menor temos:

$\displaystyle sen(x)=\frac{\overline{AC}}{\overline{OC}}=\frac{\overline{AC}}{1}$ .

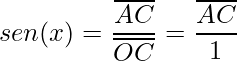Então,

$\overline{AC}=sen(x)$ .

2) Uma vez que temos um ângulo de $x$ radianos, arco circular de raio 1 e sabendo que uma volta completa possui $2\pi$ radianos com comprimento $2\pi r$ . Logo, ao fazer uma regra de três obtemos

$B\hat{O}C=x$ .

3) Considerando o triângulo maior temos:

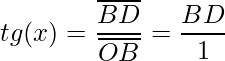$\displaystyle tg(x)=\frac{\overline{BD}}{\overline{OB}}=\frac{BD}{1}$ . Assim,

$\overline{BD}=tg(x)$ .

Então, substituindo tem-se:

$sen(x)\leq x\leq tg(x)$ .

Além disso, dividindo todos os termos por $sen(x)$ obtém-se:

$\displaystyle 1 \leq \frac{x}{sen(x)}\leq \frac{1}{cos(x)}$ .

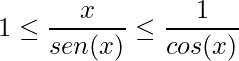Logo, invertendo todas as frações fica-se com:

$\displaystyle 1 \geq \frac{sen(x)}{x}\geq cos(x)$ .

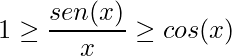Assim, aplicando o limite em todos os termos para $x\rightarrow 0$

$\displaystyle\lim\limits_{x\rightarrow 0}1\geq \lim\limits_{x\rightarrow 0}\frac{sen(x)}{x}\geq \lim\limits_{x\rightarrow 0}cos(x)$ .

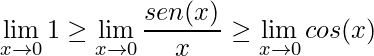Por conseguinte, tem-se:

$\displaystyle 1\geq \lim\limits_{x\rightarrow 0}\frac{sen(x)}{x}\geq 1$ .

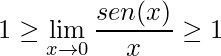Portanto, pela Propriedade dos Limites nº 11 chega-se a

$\displaystyle \lim\limits_{x\rightarrow 0}\frac{sen(x)}{x}=1$ .

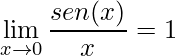2º Limite Fundamental

$\displaystyle \lim\limits_{x\rightarrow \pm \infty}\left(1+\frac{1}{x}\right)^{x}=e$

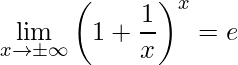
Seja a expansão binominal dada por:

$\displaystyle \left(a+b\right)^{n}=a^{n}+na^{n-1}b+\left(\frac{n(n-1)}{2!}\right)a^{n-2}b^{2}+\left(\frac{n(n-1)(n-2)}{3!}\right)a^{n-3}b^{3}+\cdots+nab^{n-1}+b^{n}$ .

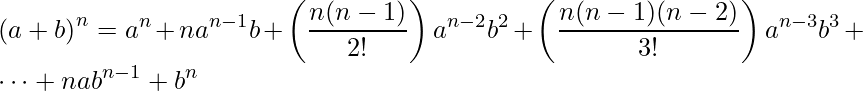Então, tem-se:

$\displaystyle \left(1+\frac{1}{n}\right)^{n}=1+1+\frac{n(n-1)}{n^{2}}\frac{1}{2!}+\frac{n(n-1)(n-2)}{n^{3}}\frac{1}{3!}+\cdots+\frac{n!}{n^{n}}\frac{1}{n!}$ .

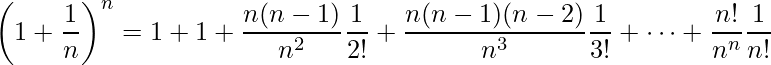Além disso, quando aplica-se o limite $n\rightarrow \pm \infty$ fica-se com:

$\displaystyle \lim\limits_{n\rightarrow \pm \infty}\left(1+\frac{1}{n}\right)^{n}=1+1+\frac{1}{2!}+\frac{1}{3!}+\cdots+\frac{1}{n!}=e$ .

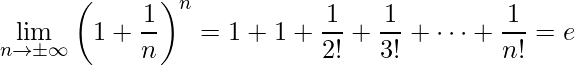Logo, chega-se ao limite que queríamos mostrar

$\displaystyle \lim\limits_{x\rightarrow \pm \infty}\left(1+\frac{1}{x}\right)^{x}=e$ .

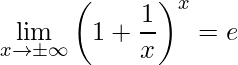Obs: Deste mesmo limite fundamental apenas fazendo uma troca de variável chega-se a:

$\displaystyle \lim\limits_{x\rightarrow \pm \infty}\left(1+\frac{1}{x}\right)^{x}=\lim\limits_{t\rightarrow 0}(1+t)^{\frac{1}{t}}=e$ .

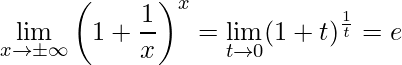3º Limite Fundamental

$\displaystyle \lim\limits_{x\rightarrow 0}\frac{a^{x}-1}{x}=\ln a$

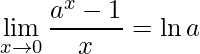
Inicia-se esta demonstração fazendo uma troca de variáveis $t=a^{x}-1\therefore a^{x}=t+1$ e quando $x\rightarrow 0$ também $t\rightarrow 0$ .

Além disso, deve-se também encontrar uma expressão em $t$ que seja igual a $x$ para substituir quando faz-se a troca de variáveis. Assim, aplicando o logaritmo neperiano tem-se:

$\displaystyle a^{x}=t+1\Rightarrow \ln a^{x}=\ln(t+1)\Rightarrow x\ln a=\ln(t+1)\Rightarrow$
$\displaystyle x=\frac{\ln(t+1)}{\ln a}$ .

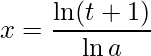Logo, escreve-se:

$\displaystyle \lim\limits_{x\rightarrow 0}\frac{a^{x}-1}{x}=\lim\limits_{t\rightarrow 0}\frac{t}{\frac{\ln(t+1)}{\ln a}}$ .

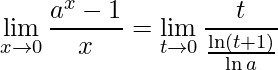Por conseguinte, aplicando as Propriedade dos Limites obtém-se:

$\displaystyle \lim\limits_{t\rightarrow 0}\frac{t}{\frac{\ln(t+1)}{\ln a}}=\ln a\cdot \lim\limits_{t\rightarrow 0}\frac{t}{\ln(t+1)}\Rightarrow \ln a\cdot \lim\limits_{t\rightarrow 0}\frac{1}{\frac{\ln(t+1)}{t}}$ .

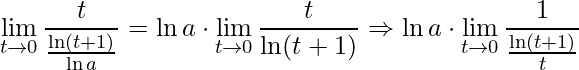Cabe ressaltar que, utilizando as propriedades dos logaritmos chega-se a:

$\displaystyle \ln a\cdot \lim\limits_{t\rightarrow 0}\frac{1}{\ln(t+1)^{\frac{1}{t}}} \Rightarrow \ln a\cdot \frac{\lim\limits_{t\rightarrow 0}1}{\lim\limits_{t\rightarrow 0} \ln(t+1)^{\frac{1}{t}}}$ .

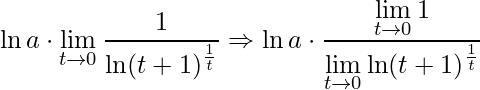Além do mais, segundo a Propriedade dos Limites nº9, pode-se inverter a ordem do limite com a do logaritmo. Por isso, fica-se com:

$\displaystyle \ln a\cdot \frac{\lim\limits_{t\rightarrow 0}1}{\lim\limits_{t\rightarrow 0} \ln(t+1)^{\frac{1}{t}}}=\ln a\cdot \frac{1}{\ln \lim\limits_{t\rightarrow 0}(t+1)^{\frac{1}{t}}}$ .

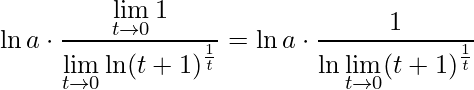Como consequência do 2º Limite Fundamental conforme vimos acima tem-se:

$\displaystyle \ln a\cdot \frac{1}{\ln e}=\ln a\cdot \frac{1}{1}=\ln a$ .

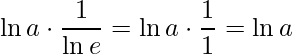Então,

$\displaystyle \lim\limits_{x\rightarrow 0}\frac{a^{x}-1}{x}=\ln a$ .

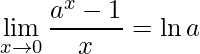Portanto, espero que tenham gostado do Post sobre Limites Fundamentais. Continuem nos acompanhando. Compartilhem esse Post. Se ficou mais alguma dúvida coloque nos comentários abaixo utilizando seu perfil do Facebook.

Além disso, dê continuidade aos seus estudos acompanhando a resolução de alguns exercícios em que utiliza-se este Limite Fundamental clicando aqui ou assista mais resoluções em vídeos clicando aqui.

Limites Fundamentais

Baixe de forma gratuita nossos Ebooks e treinamentos

Limites Fundamentais

1º Limite Fundamental

2º Limite Fundamental

3º Limite Fundamental

Compartilhe agora mesmo:

Construindo gráficos de funções online

Resolvendo Integral usando duas técnicas: Integração por partes e Integração por substituição

Cálculo do volume dos sólidos de revolução

Para enviar seu comentário, preencha os campos abaixo:

Deixe um comentário Cancelar resposta

Seja o primeiro a comentar!

Damos valor à sua privacidade

Cookies estritamente necessários

Cookies de desempenho

Cookies de funcionalidade

Cookies de publicidade

Baixe de forma gratuita nossos Ebooks e treinamentos

Limites Fundamentais

1º Limite Fundamental

2º Limite Fundamental

3º Limite Fundamental

Compartilhe agora mesmo:

Construindo gráficos de funções online

Resolvendo Integral usando duas técnicas: Integração por partes e Integração por substituição

Cálculo do volume dos sólidos de revolução

Para enviar seu comentário, preencha os campos abaixo:

Deixe um comentário Cancelar resposta

Seja o primeiro a comentar!

Damos valor à sua privacidade

Cookies estritamente necessários

Cookies de desempenho

Cookies de funcionalidade

Cookies de publicidade

Faça aulas personalizadas sobre conteúdos específicos de Matemática e Raciocínio Lógico