Limites Infinitos e Limites no Infinito
Neste post apresenta-se a temática dos Limites Infinitos e Limites no Infinito, que consiste nos casos em que o limite em um determinado ponto resulta em ![]() e nos casos em que queremos saber o limite quando
e nos casos em que queremos saber o limite quando ![]() .
.
Antes de começarmos a explicar estes dois conteúdos apresentam-se as operações que envolvem ![]() e que possuem valores reais, ao contrário das operações que geram indeterminação.
e que possuem valores reais, ao contrário das operações que geram indeterminação.
Considerando ![]() e com
e com ![]() sendo uma constante tem-se:
sendo uma constante tem-se:
| se |
se |
| se |
se |
| se |
se |
| |
Dito isto, prosseguimos as explicações trazendo dois cálculos de limites a partir da mesma função:
Exemplo 1: 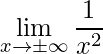
Este primeiro exemplo trabalha com a ideia de dividir uma constante qualquer por um número muito grande (positivo ou negativo).
Assim, quanto maior for este número, mais próximo de 0 estará o resultado desta divisão. Portanto, ao aplicar o limite que tende ao infinito (positivo ou negativo) obtém-se:
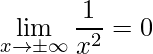 .
.
Outros exemplos onde aplica-se a mesma ideia são:
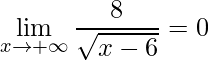
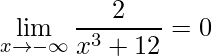 .
.
Exemplo 2: 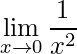
O segundo exemplo é oposto ao primeiro, pois o denominador está tendendo a zero, ou seja, um número muito pequeno.
Obs: Deve-se tomar cuidado quando trabalha-se com limites em que o denominador tende a 0, pois pode ocorrer que os valores muito próximos ao ponto desejado (pela direita e pela esquerda) possuam sinais contrários.
No nosso exemplo não há este problema, porque a função possui expoente par tornando os valores sempre positivos. Assim, quando dividimos uma constante positiva por um número que tende a 0, resulta em um número que tende à ![]() :
:
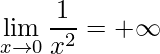 .
.
Outros exemplos onde aplica-se a mesma ideia são:
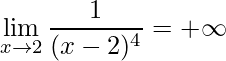
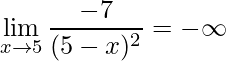
Assim, espero que tenham gostado desse post sobre Limites Infinitos e Limites no Infinito. Continuem nos acompanhando, compartilhe esse post. Qualquer dúvida deixe nos comentários abaixo usando seu login do facebook. Veja também a explicação mais detalhada em vídeo clicando aqui.



Deixe um comentário