Exercícios resolvidos sobre limites fundamentais
Neste post apresentam-se alguns Exercícios resolvidos sobre limites fundamentais, caso você ainda não os conhece clique aqui.
Exemplo 1) 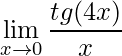
Neste primeiro exercício inicia-se utilizando as propriedades trigonométricas transformando a função tangente na divisão de seno por cosseno da seguinte forma:
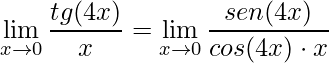 .
.
Em seguida, deve-se multiplicar numerador e denominador por 4 e aplicar a propriedade da multiplicação de limites, acompanhe:
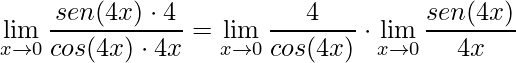 .
.
Agora pode-se trabalhar com os dois limites separadamente e, no fim, multiplicar as suas respostas. No primeiro vê-se facilmente que quando ![]() o denominador tenderá a 1, pois
o denominador tenderá a 1, pois ![]() :
:
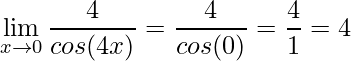 .
.
N segundo limite deve-se fazer uma mudança de variável, onde ![]() , sabendo que quando
, sabendo que quando ![]() temos também
temos também ![]() . Assim:
. Assim:
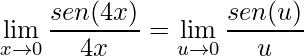 .
.
Aplicando o limite fundamental visto no post anterior tem-se:
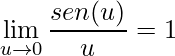 .
.
Por fim, deve-se multiplicar o resultado dos dois limites, onde obtém-se:
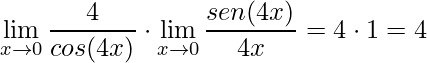 .
.
Exemplo 2) 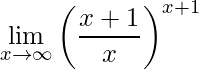
Ao olharmos para este segundo exemplo já podemos perceber que ao manipular este limite chega-se em uma expressão semelhante ao segundo limite fundamental.
Utilizando as propriedades das potências tem-se:
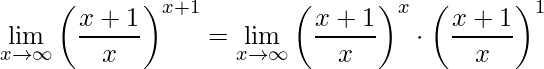 .
.
Como no exemplo anterior separa-se o limite na multiplicação de dois limites e depois de resolve-los, separadamente, multiplicam-se os resultados:
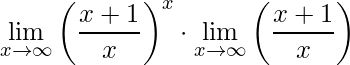 .
.
Manipulando o primeiro limite percebe-se facilmente que tem-se um limite fundamental:
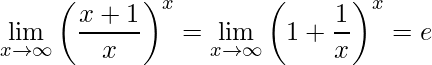 .
.
O segundo, manipulando e usando as propriedades dos limites tem-se:
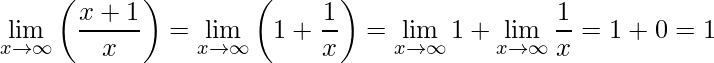 .
.
Por fim, basta multiplicar os resultados:
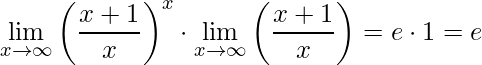 .
.
Exemplo 3) 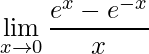
Neste exemplo inicia-se fazendo um truque matemático de somar e subtrair 1 do numerador e, em seguida, separar este limite na soma de outros dois:
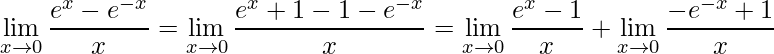 .
.
O primeiro é aplicação direta do 3º limite fundamental:
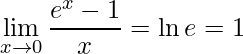 .
.
O segundo deve-se manipular ele, onde chega-se a:
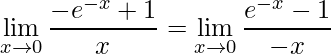 .
.
Agora fazendo uma troca de variável, ![]() e sabendo que quando
e sabendo que quando ![]() também
também ![]() , substituindo tem-se:
, substituindo tem-se:
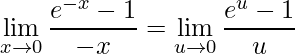 .
.
Nota-se novamente o 3º limite fundamental:
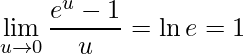 .
.
Somando os dois limites tem-se:
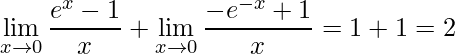 .
.



Deixe um comentário