Exemplos de Máximos e Mínimos de uma função
Neste post apresentam-se Exemplos de Máximos e Mínimos de uma função, primeiramente exemplo teórico e em seguida um exemplo prático de aplicação deste conteúdo.
Exemplo 1: Encontre os pontos de máximos e mínimos da função dada:
![]() com
com ![]() .
.
Sabemos que f é diferenciável por ser uma função polinomial, assim pode-se derivar e encontrar os pontos críticos da função da seguinte forma:
![]() .
.
Calculando os pontos críticos: ![]() onde encontramos em
onde encontramos em ![]() . Estudando o sinal antes e depois do ponto crítico tem-se:
. Estudando o sinal antes e depois do ponto crítico tem-se:
![]() ;
;
![]() .
.
Como há mudança de sinal pode-se afirmar que este é um ponto de máximo ou mínimo, e ao avaliar os pontos no entorno fica-se com:
![]() ;
;
![]() ;
;
![]() .
.
Assim, concluímos que este é um ponto de mínimo absoluto, visto que ela é continua e não há outros pontos de inflexão. Podemos também concluir que não a pontos de máximo pois a função tende nas suas extremidades para ![]() .
.
Exemplo 2: Suponha que o número de bactérias em uma cultura no instante t é dada por 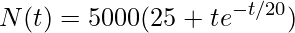 . Ache o maior e o menor número de bactérias durante o intervalo de tempo
. Ache o maior e o menor número de bactérias durante o intervalo de tempo 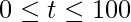 .
.
Este exemplo possui domínio fechado. Assim, no cálculo dos máximos e mínimos devemos observar, além dos pontos críticos, os pontos extremos do domínio.
Iniciamos encontrando os possíveis pontos críticos a partir da primeira derivada e igualando a zero, na derivação devemos utilizar a derivada do produto:
![]() ,
,
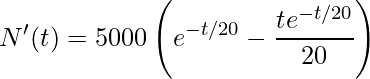 .
.
Em seguida, deve-se igualar a zero, ![]() :
:
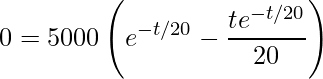
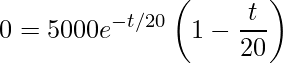
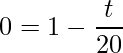
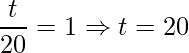 .
.
Por fim, deve-se calcular o número de bactérias nos extremos e no ponto crítico. Para assim concluirmos quais são os pontos de máximo e mínimo dentro do intervalo adotado:
![]() ;
;
![]() ;
;
![]() .
.
Portanto, temos como o menor número de bactérias 125000 e como o maior número de bactérias 161787,94 no intervalo indicado. O gráfico do número de bactérias em função do tempo é o seguinte:

Assista um exemplo em vídeo clicando aqui.

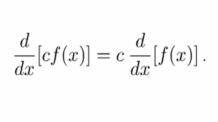



Deixe um comentário