Função matemática

Além do contexto de sala de aula, as funções matemáticas estão frequentemente presentes em nossas vidas e nem nos damos conta. Elas são definidas como certas relações entre duas ou mais grandezas.

Ainda não ficou claro? Vou dar dois exemplos que provavelmente você faça diariamente e não perceba. Quando você vai à padaria comprar pão, o valor a ser pago está relacionado ao peso do pão, não é verdade? Então podemos dizer que o valor está em função do seu peso.

Vou dar outro exemplo, porém este envolvendo muito mais variáveis. O tempo que você leva para ir à universidade/escola/trabalho está em função da velocidade do veiculo (carro, ônibus, moto,…) que transporta você, em função da quantidade de veículos que se encontram nas ruas, em função do número de lombadas e semáforos, …, entre outras tantas variáveis.  

Já no contexto escolar ou acadêmico, as funções aparecem em geral na matemática, na física, nas engenharias, sobretudo nas disciplinas de Cálculo. Iniciamos abordando funções que dependem apenas de uma variável, como no nosso primeiro exemplo do valor do pão.

Em geral, trabalhamos com a variável x , como variável independente, e a f(x), como variável dependente, que se lê como função de x. O conjunto de todos valores em que x pode assumir chamamos de domínio. Já o conjunto onde estão os valores produzidos pela função f(x) chamamos de imagem.

Exemplo de Função matemática

Por exemplo, no caso apresentado anteriormente, da compra de pão, supomos que o valor a quilo esteja R$ 6,50, então tem-se a função:

,

onde x representa a quantidade de quilo e f(x) o valor a ser pago. Neste nosso problema o domínio são todos os valores não negativos, visto que não existe peso negativo. Da mesma forma a imagem são também valores não negativos.

Muitas vezes para uma melhor visualização do comportamento destas duas variáveis, constrói-se o gráfico das funções. Ou seja, no plano Cartesiano um eixo representa os valores de x e o outro os valores de f(x).

Na figura a seguir, plotamos o gráfico da compra do pão, onde o eixo x representa o peso em Kg e y=f(x) o representa o valor em reais:

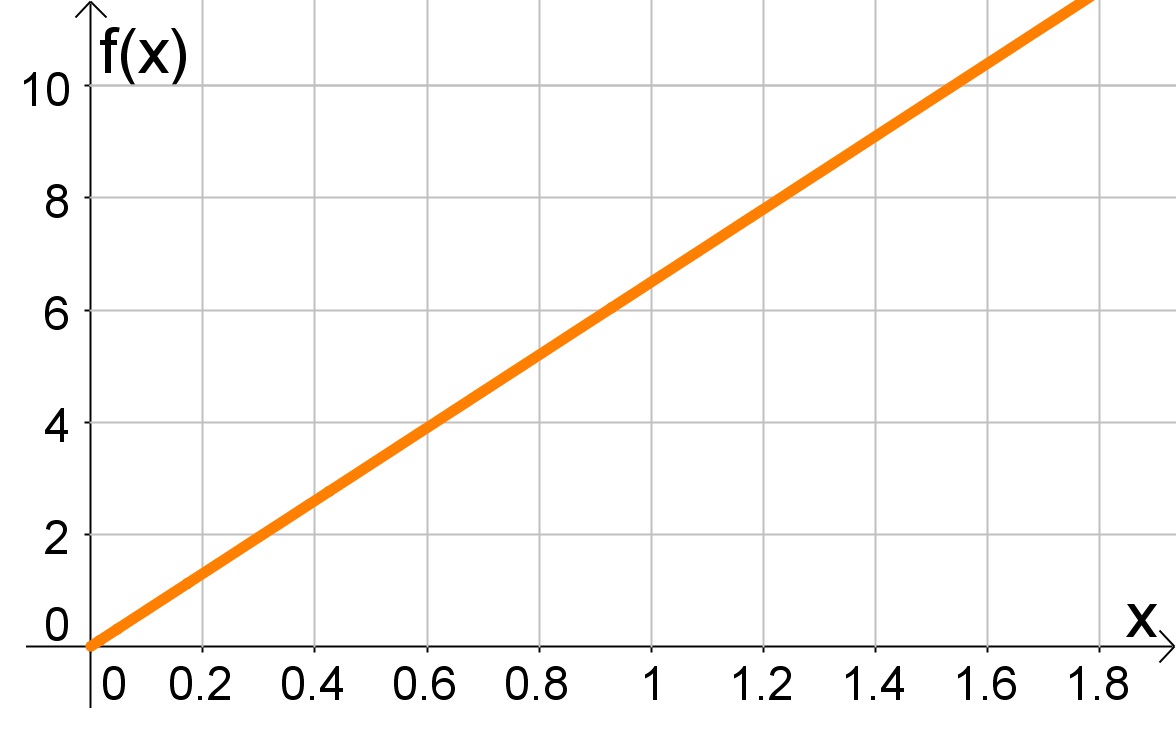
Continue seu estudo de Função matemática com o tema Domínio e Imagem, clicando aqui.