Função do 2 grau – definição
Neste post apresentamos a definição e características da Função do 2 grau, que é um dos tipos de Função Potência. Ela também é conhecida como Função quadrática, e é representada graficamente através de uma parábola.
Este tipo de função é encontrada em diversas aplicações, como por exemplo, na equação que descreve o movimento de queda livre, o lançamento de um projétil e o Índice de Massa Corpórea (IMC). Ela é encontrada também em algumas aplicações da engenharia civil, na economia, entre outras áreas de estudo.
Definição:
Uma função ![]() é chamada de função 2º grau quando existem números reais
é chamada de função 2º grau quando existem números reais ![]() ,
, ![]() e
e ![]() com
com ![]() , tais que
, tais que
![]()
para todo ![]() .
.
Exemplos de Função do 2 grau:
1)
, em que
,
e
;
2)
em que
,
e
;
3)
em que
,
e
.
Características de uma Função do 2 grau:
Cada um deste coeficientes (a,b e c) fornecem informações sobre a equação:
-
Coeficiente a:
O coeficiente a é aquele que dá a principal característica das funções quadráticas que é a concavidade da parábola.
Se a>0 então a concavidade é voltada para cima.
Se a<0 então a concavidade é voltada para baixo.
Veja o exemplo a baixo.
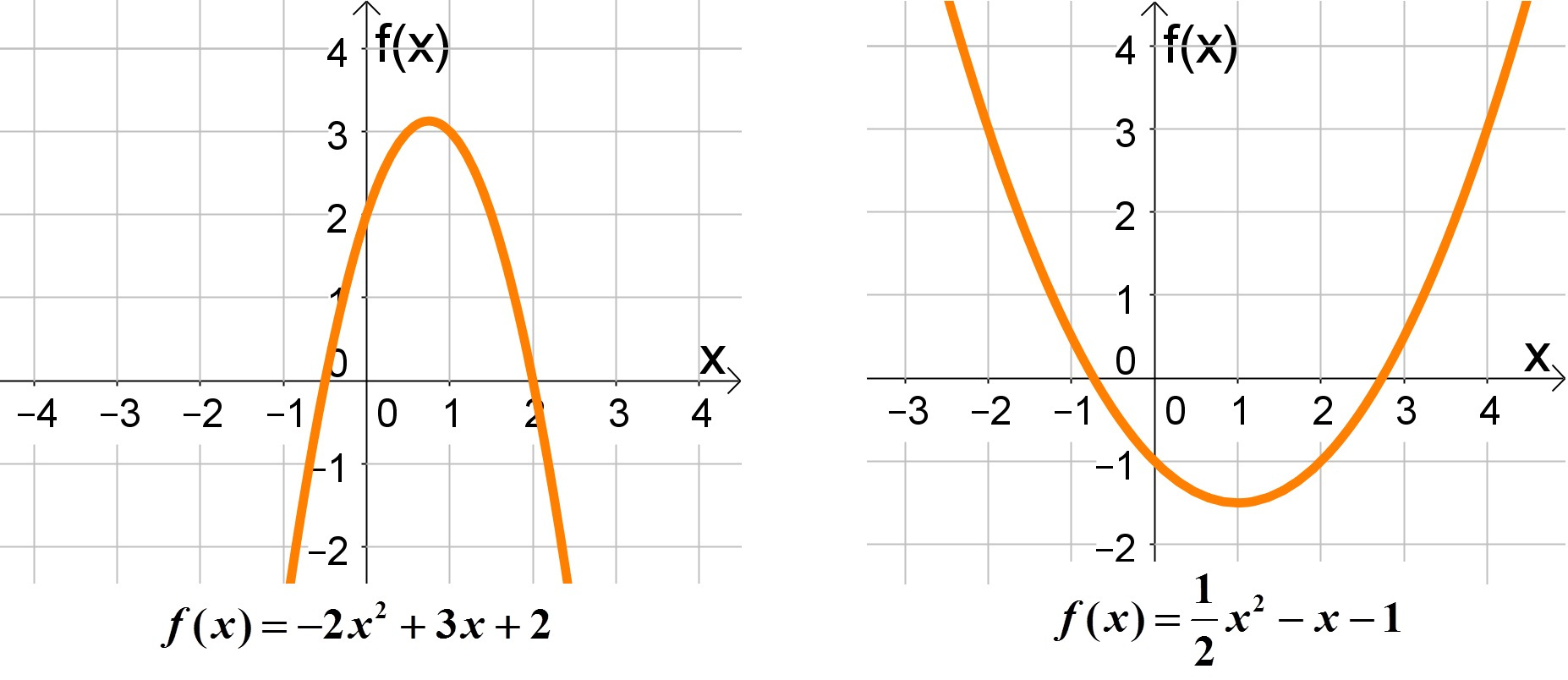
Outro aspecto é que o coeficiente a representa a abertura da concavidade, quando maior for o valor em modulo de a, maior será a abertura.
-
Coeficiente b:
O sinal deste coeficiente representa o comportamento do gráfico ao interceptar o eixo y:
se b>0 então o gráfico é crescente ao interceptar o eixo y.
se b<0 então o gráfico é decrescente ao interceptar o eixo y.
Observe no exemplo acima.
-
Coeficiente c:
O valor do coeficiente c representa o valor de y=f(x) no ponto onde o gráfico intercepta o eixo y, assim temos o ponto (0,c).
- Vértice da função:
O vértice de uma função do 2 grau representa o ponto de máximo, se a<0, ou o ponto de mínimo, se a>0, do gráfico da função. Este ponto é dado por:
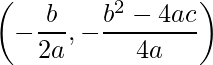 .
.
- Raízes da função:
As raízes das funções do segundo grau são os pontos onde a função intercepta o eixo x, mas cuidado, isto ocorre somente se as raízes possuírem valores reais. Caso contrário o gráfico não intercepta o eixo x.
Deste modo, como as raízes são pontos onde o gráfico corta o eixo x, então seus respectivos valores em y=f(x) são iguais a zero. Assim os valores em x podem ser encontradas por diversas formas, talvez a mais conhecida seja a Fórmula de Bhaskara, mas podemos usar também Método da Soma e Produto ou outra forma que preferir.
Usando a Fórmula de Bhaskara temos as raízes ![]() e
e ![]() :
:
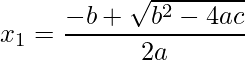
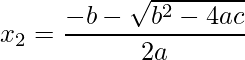 .
.
Continue seus estudos de Função do 2 grau com exercícios resolvidos, clicando aqui.

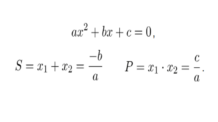

Deixe um comentário