Função do 2 grau – exercícios resolvidos passo a passo
Este post é uma continuação daquele em que apresentamos a definição e características da Função do 2 grau, deste modo, continuaremos com a Função do 2 grau – exercícios resolvidos passo a passo.
Para iniciar, reapresenta-se a definição deste tipo de função:
Uma função ![]() é chamada de função 2º grau quando existem números reais
é chamada de função 2º grau quando existem números reais ![]() ,
, ![]() e
e ![]() com
com ![]() , tais que
, tais que
![]()
para todo ![]() .
.
Exercícios de Função do 2 grau:
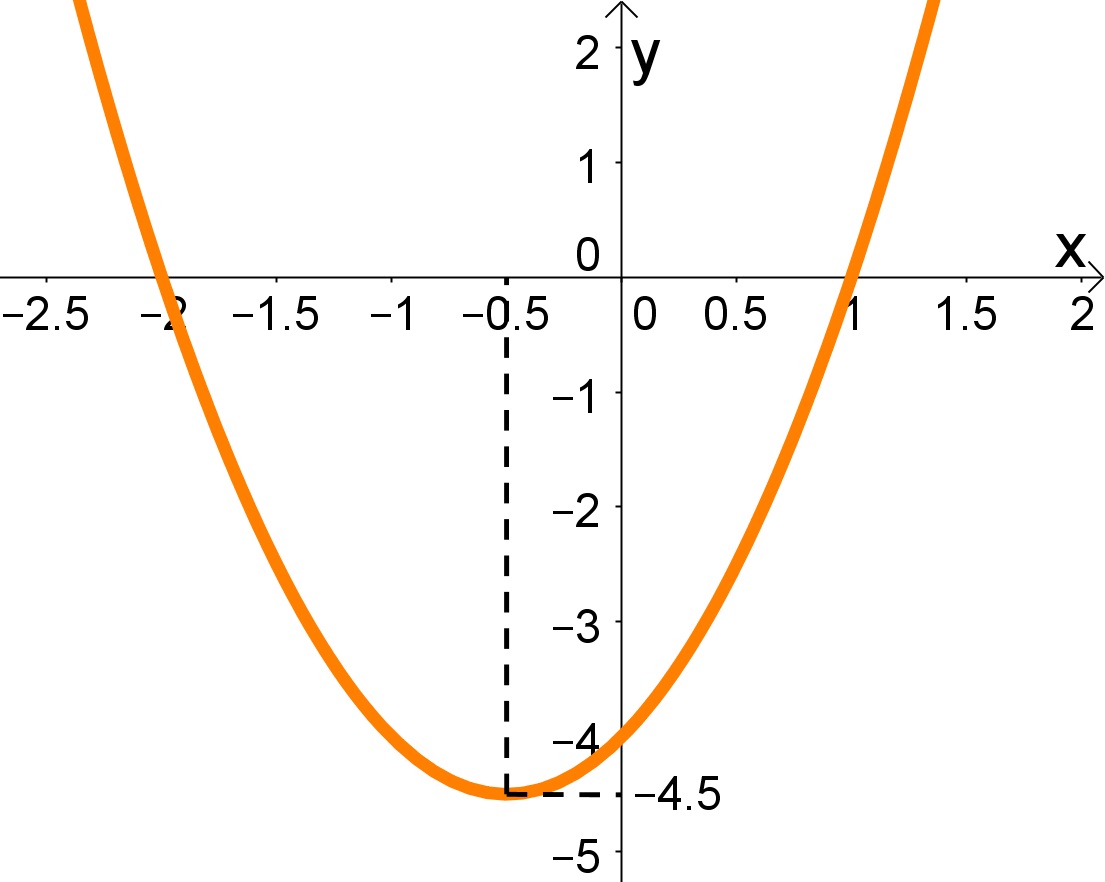
1) Construa o esboço da função 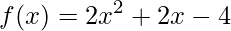 , a partir das características desta função.
, a partir das características desta função.
Iniciamos observando as informações fornecidas pelos coeficientes a,b e c:
- O coeficiente a=2 nos diz que a concavidade da parábola está voltada para cima, pois a>0.
- O coeficiente b=2 nos diz que o gráfico ao interceptar o eixo y de forma crescente, pois b>0.
- O coeficiente c=-4 nos diz que o ponto onde o gráfico intercepta o eixo y.
Com estas informações já podemos ter uma ideia do gráfico da função:
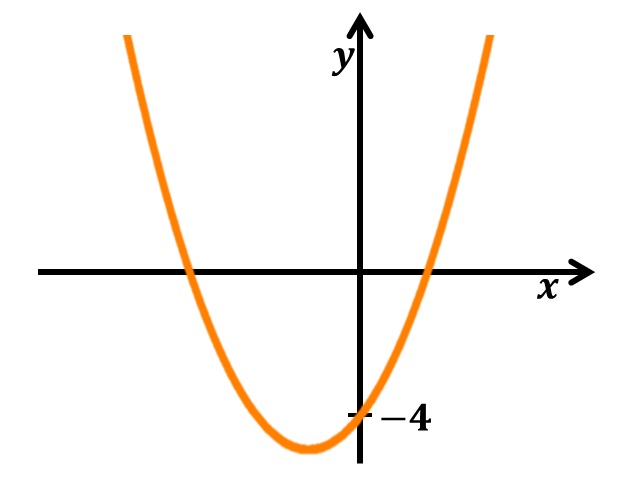
Como tem-se uma parábola voltada para cima, o vértice desta uma função do 2 grau é um ponto de mínimo. Este ponto é dado por:
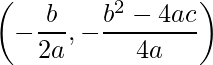 .
.
Substituindo encontra-se:
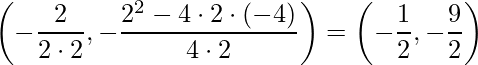 .
.
Por fim, encontraremos as Raízes da função desta função segundo grau utilizando conhecida seja a Fórmula de Bhaskara. Lembre-se que as raízes são os pontos onde a função intercepta o eixo x.
Usando a Fórmula de Bhaskara temos as raízes ![]() e
e ![]() :
:
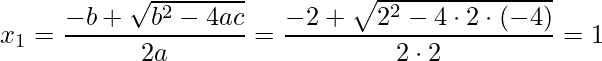
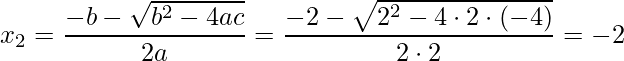 .
.
Com mais estas informações podemos construir um esboço mais completo do gráfico da função dada:
1) Construa a função geradora do gráfico presente na figura a seguir.
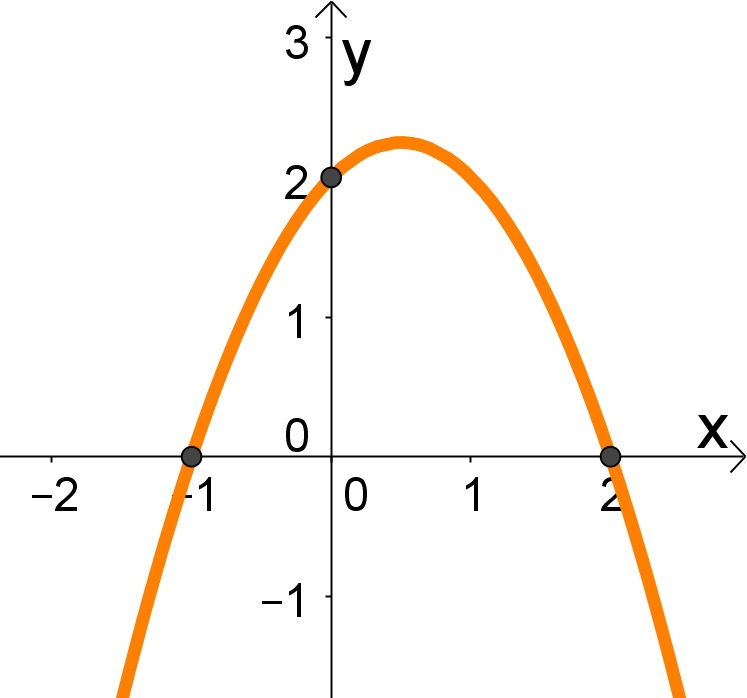
Observando a figura podemos extrair dela 3 pontos, as raízes (-1,0) e (2,0) e o ponto onde intercepta o eixo y, (0,2). Assim, já temos a informação do coeficiente c=2.
Para os outros coeficientes utilizamos a fórmula geral, ![]() e é possível construir um sistema linear. Com o ponto (-1,0) e c=2 temos:
e é possível construir um sistema linear. Com o ponto (-1,0) e c=2 temos:
![]()
e com o ponto (2,0) e c=2
![]() .
.
Assim, obtém-se
![]()
![]() ,
,
resolvendo este sistema encontraremos a=-1 e b=1, desta forma, a equação que descreve o gráfico acima é dada por:
![]() .
.
Continue seus estudos de funções clicando aqui.

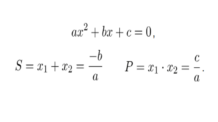

Deixe um comentário