Funções exponenciais e suas características

As Funções exponenciais são muito utilizadas nos estudos que envolvem o crescimento de certas populações. Um exemplo é o crescimento da população das bactérias que, através da divisão celular, faz o seu número de células iniciais crescer de forma exponencial.

Este tipo de função é encontrada sobretudo em fenômenos biológicos, mas as funções exponenciais podem ser encontradas em outras áreas como: 

• Na economia: A maioria dos investimentos são calculados a partir de juros compostos, na qual a taxa de juros é descrita na forma exponencial. 

• Na ciência da informação: Ao postar uma informação, principalmente em redes sociais, ela se difunde de forma exponencial, visto que seus usuários recebem e compartilham para outros usuários instantaneamente.

• Na física nuclear: A fissão nuclear do urânio 235 é expressa de forma exponencial, visto que a cada átomo fissionado são liberados em média 3 novos nêutrons, que por sua vez, irão provocar a fissão de outros átomos.  

Definição da função exponencial:

Uma função é chamada de função exponencial quando existem números reais (com ) e tais que 

para todo  .

Exemplos:

1) ;

2) ;

3) .

Características das Funções exponenciais:

A combinação dos coeficientes a e b determina se a função será crescente ou decrescente.

• Crescente

Se 0<a<1 e b<0 ou se 1<a e 0<b.

• Decrescente

Se 0<a<1 e 0<b ou se 1<a e b<0.

Observe este comportamento nos gráficos a seguir:

Observação: Caso a função exponencial for multiplicada por uma constante c da forma:

ela produzirá uma alongamento na função se c>1 ou se 0<c<1 a função será comprimida.

Entretanto, se c for um valor negativo ocorrerá um espelhamento em relação ao eixo x, respeitando as mesmas regras dos valores positivos, ou seja, a função será alongada se c<-1 e comprimida se -1<c<0. 

Ademais, cabe salientar que o valor de c correspondo o ponto onde a função intercepta o eixo y. Observe no exemplo a baixo:

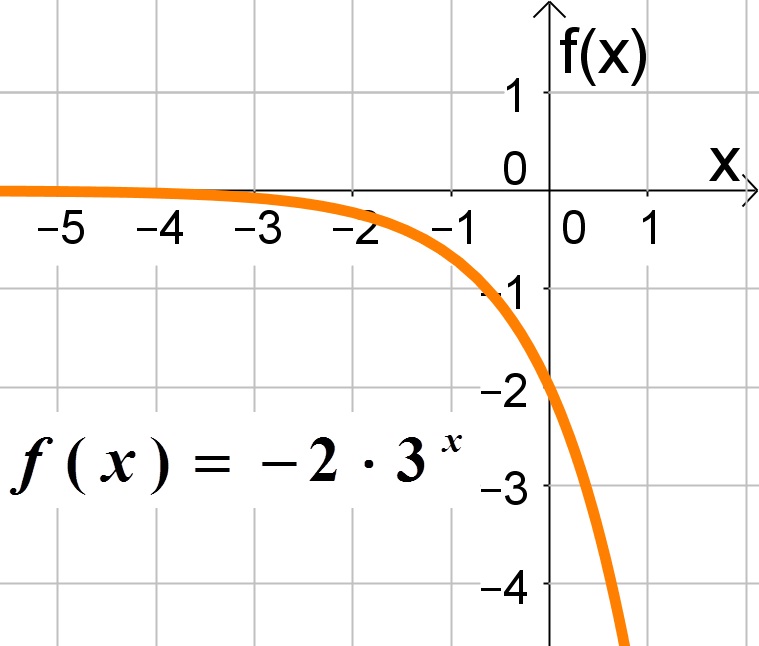
Continue seus estudos de funções clicando aqui.