Funções logarítmicas e suas características
As Funções logarítmicas são as funções em que utilizam na sua lei de formação o operador logaritmo. Como o logaritmo é a operação inversa da exponencial, seus respectivos tipos de função também são inversas uma da outra. Por este motivo as Funções logarítmicas são na maioria das vezes utilizadas nas mesmas áreas de aplicações.
Uma aplicação muito interessante das funções logarítmicas é a medição da magnitude dos abalos sísmicos (terremotos). A escala Richter que classifica a magnitude dos terremotos utiliza uma função logarítmica na base 10.
As funções logarítmicas são utilizadas também no calculo da magnitude aparente e absoluta (brilho) de um corpo celeste, este cálculo é útil para determinar a distância deste corpo ao planeta Terra.
Definição da função logarítmica:
Uma função ![]() é chamada de função logarítmica quando existe um número real positivo
é chamada de função logarítmica quando existe um número real positivo ![]() com
com ![]() tal que
tal que
![]() ,
,
para todo ![]() , onde se lê logaritmo de x na base a.
, onde se lê logaritmo de x na base a.
Obs: Em muitos materiais didáticos pode-se encontrar um classe de logaritmo especial, que é o logaritmo natural, ou seja, quando na base temos o número natural (número de Euler)
![]() .
.
Exemplos:
1)
;
2)
;
3)
.
Muitas vezes no estudo das funções logarítmicas utilizam-se as Propriedades dos Logaritmos, como por exemplo a mudança de base, caso você necessite utilizar alguma propriedade que não recorde, clique aqui.
Características das Funções logarítmicas:
O coeficiente a determina se a função será crescente ou decrescente.
- Crescente quando a>1;
- Decrescente quando 0<a<1.
Observe este comportamento nos gráficos a seguir:
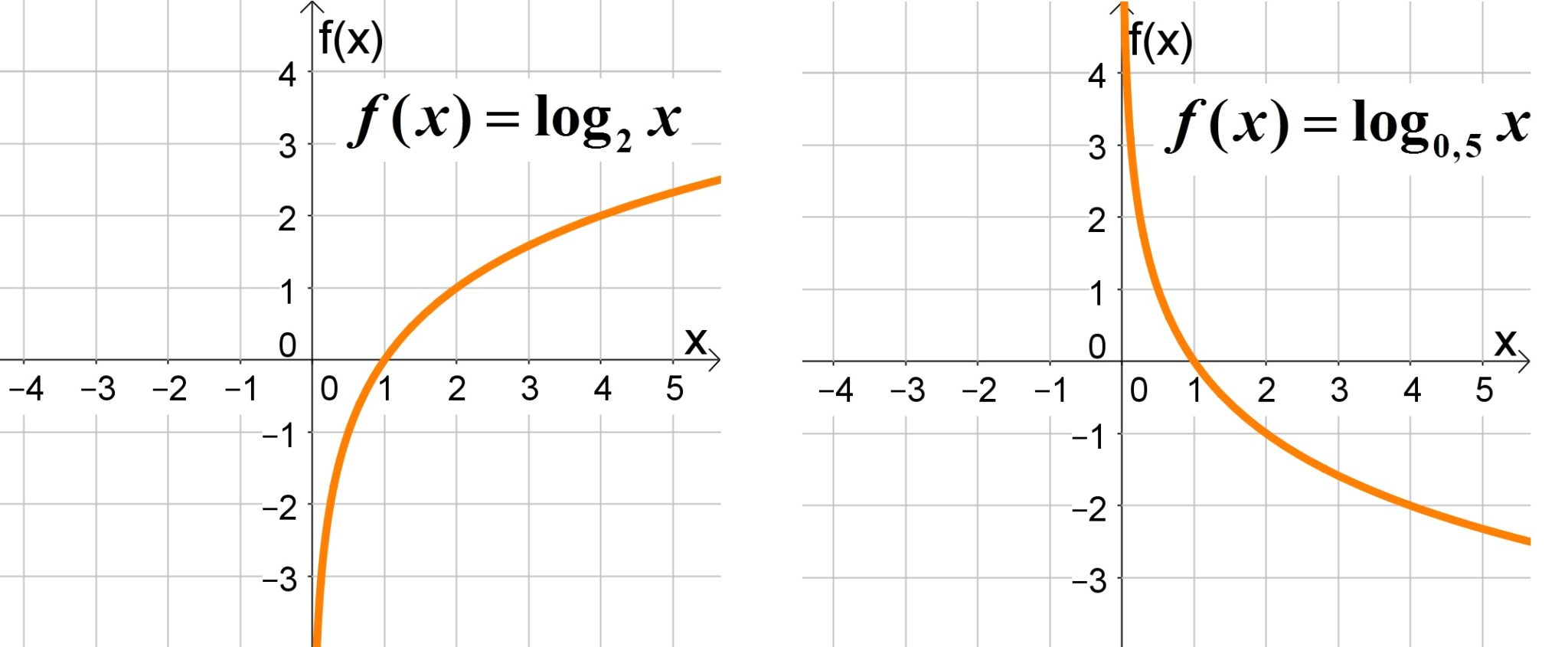
Observação: Caso a função for multiplicada por uma constante b da forma, produzirá uma alongamento na função se b>1 ou se 0<b<1 a função será comprimida.
Caso b for uma valor negativo ocorrerá um espelhamento em relação ao eixo x, respeitando as mesmas regras dos valores positivos, ou seja, a função será alongada se b<-1 e comprimida se -1<b<0.
A função na sua forma básica ![]() intersecta o eixo das abscissas no ponto (1,0). Caso somarmos uma constante c no logaritmando, esta produzirá um deslocamento horizontal no gráfico.
intersecta o eixo das abscissas no ponto (1,0). Caso somarmos uma constante c no logaritmando, esta produzirá um deslocamento horizontal no gráfico.
Se c for positivo o gráfico será deslocado para esquerda e se for negativo será deslocado para a direita. Observe os exemplos a baixo:
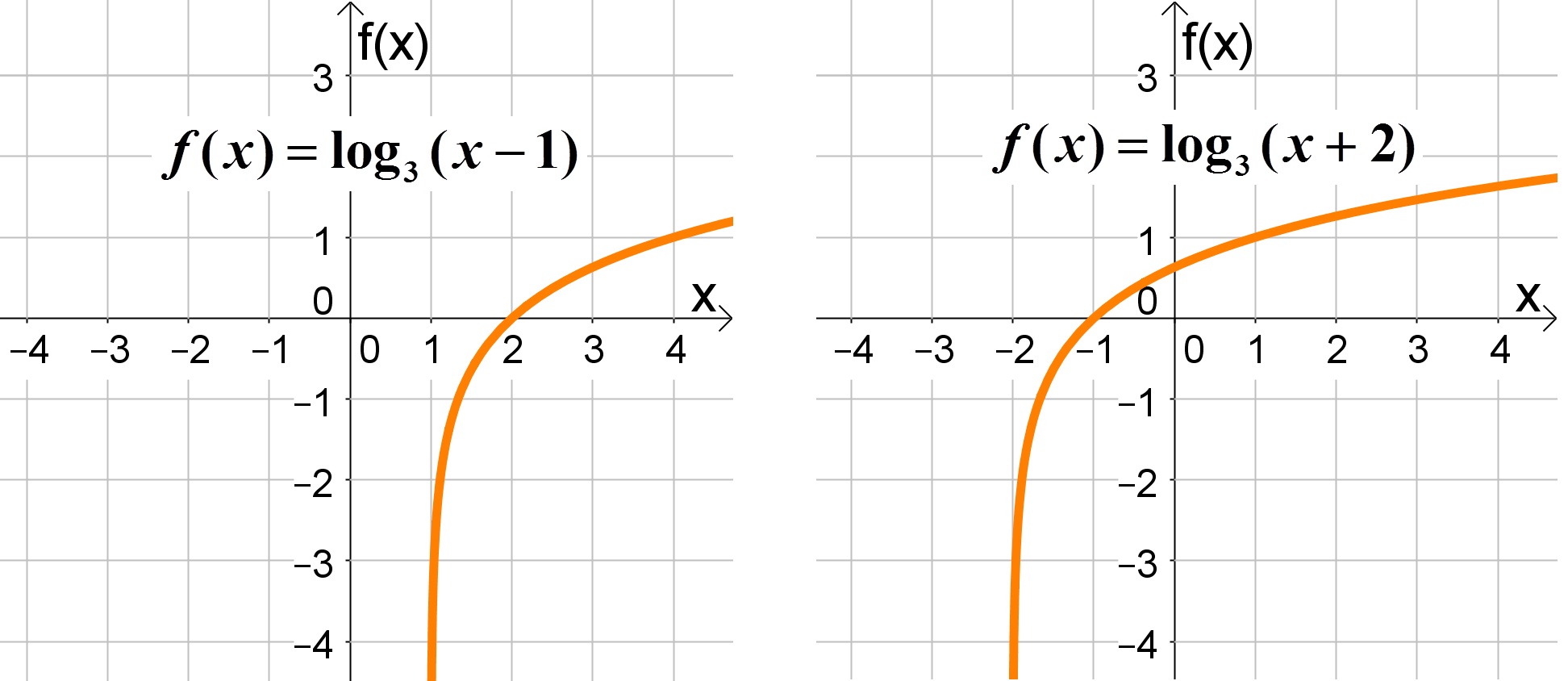
Continue seus estudos de funções clicando aqui.

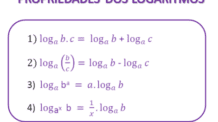

Deixe um comentário