Limites exercícios resolvidos – limites indeterminados

Este post dedica-se a limites exercícios resolvidos, na qual utilizam-se algumas técnicas para superar as formas de indeterminação. Para esse desenvolvimento será necessário fazer uso das propriedades dos limites e limites fundamentais, caso você ainda não os tenha visto este é o momento oportuno.

Exercícios resolvidos de limites

Determine os seguintes limites:

1) 

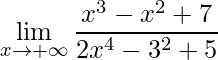
Sempre que temos um limite para resolver, devemos iniciar aplicando o limite, pois nem sempre chegamos a uma indeterminação

. 

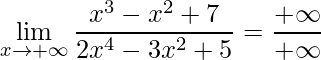Como obtemos uma forma de indeterminação, temos que utilizar alguma técnica para superá-la. Neste caso opta-se em colocar o termo de maior grau em evidência 

.

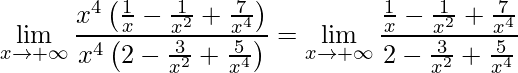e, em seguida, aplicar o limite onde encontra-se:

.

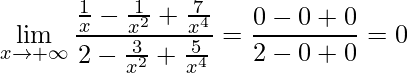2) 

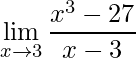
Ao aplicar o limite chegamos em outra forma de indeterminação 

.

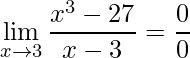Neste execício utiliza-se a fatoração do polinômio no produto de suas raízes, visto que o termo do numerador pode ser escrito em um produto 

.

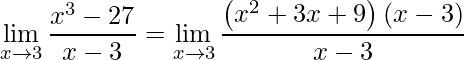Para concluir devemos simplificar os termos em comum e aplicar o limite 

.

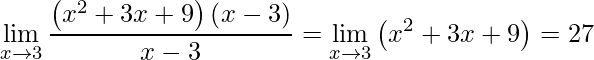3) 

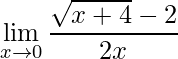
Ao aplicar o limite obtemos novamente uma indeterminação 

.

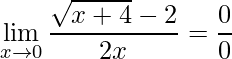Neste exercício aplica-se a técnica da racionalização que consiste em multiplicar o numerado e denominador pelo termo inverso daquele que contém a raiz 

,

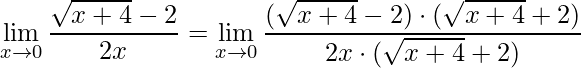onde temos o produto da diferença, assim obtém-se:

.

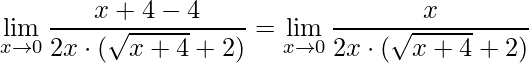Simplificando e aplicando o limite obtém-se:

. 

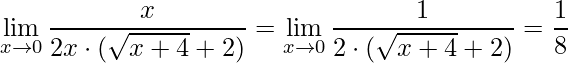4) 

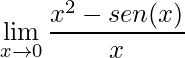
Aplicando o limite temos o seguinte tipo de indeterminação 

.

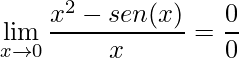Neste exercício sugerimos duas forma de solução

a) Usando as propriedades de limite e o limite fundamental:

Iniciamos aplicando a propriedade da soma dos limites 

,

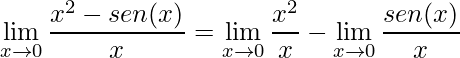observe que o segundo limite é um dos tipos de limite fundamental, assim temos 

. 

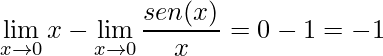b) Usando a Regra de L’Hospital:

Como temos uma indeterminação do tipo 0/0 podemos utilizar a Regra de L’Hospital, porém esta regra nos exige conhecimentos de derivadas.

A regra de L’Hospital nos diz que 

.

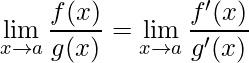Assim, aplicando as derivadas no numerador e no denominador obteremos 

.

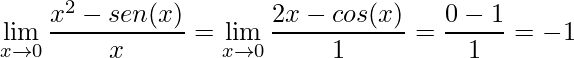Continue seus estudos fazendo uma prova online de limites, ou ainda, assistindo uma aula de limites em vídeo clicando aqui.