Definição de limites laterais

Ao calcular limite de algumas funções, percebemos que seus comportamento é diferente de lado e de outro. Assim, temos a necessidade de calcular o limite de cada lado separadamente. Para esta metodologia chamamos de cálculo dos limites laterais. Iniciaremos este post apresentando a Definição de limites laterais, em seguida, a relação que há entre os limites laterais e o limite da função em um determinado ponto, também chamado de limite bilateral.

 Definição de limites laterais

O cálculo dos limites laterais consiste determinar o limite quando nos aproximamos ora pela direita ora pela esquerda. Ou seja, o limite de uma função por valores maiores do que o ponto limite (direita)  e menores (esquerda).

Limite a direita

Se  tende quando  através de valores maiores que diz-se que é o limite de quando tende para pela direita e indica-se por:

.

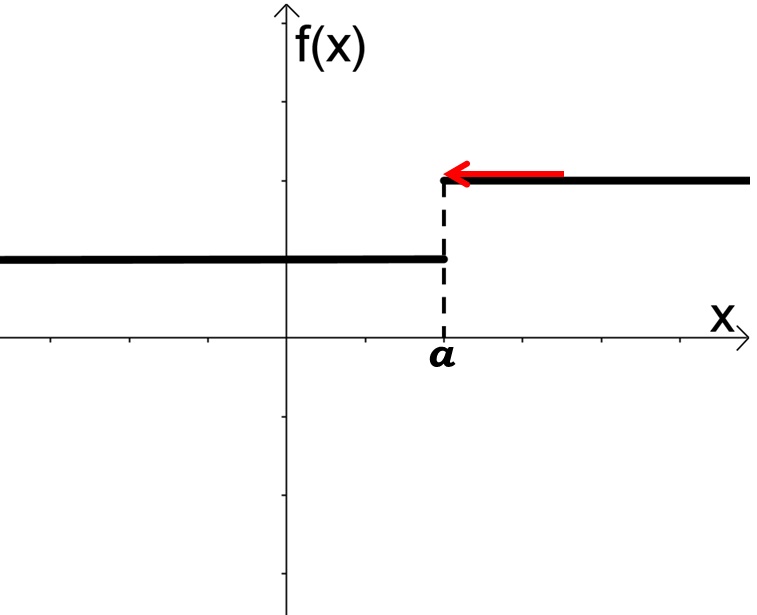
Limite a esquerda

Se  tende quando  através de valores menores que diz-se que é o limite de quando tende para pela esquerda e indica-se por:

.

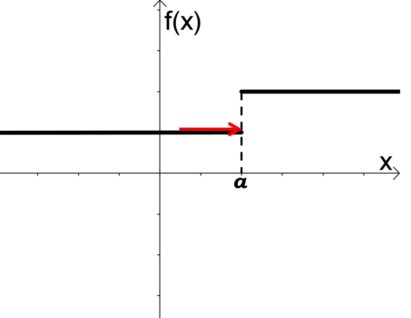
 Relação entre os limites laterais e o limite da função

Dizemos que o limite de uma função existe se e somente se os limites laterais são igual, ou seja, quando  ,

.

Caso os limites laterais forem diferentes em um determinado ponto, o limite neste ponto não existe. Como exemplo podemos observar a função apresentada nas figuras acima.

Observação 1: para o limite existir não é necessário que os limites laterais sejam iguais da função no ponto. Ou seja, f(a) pode ser diferente dos limites laterias em a. 

Observação 2: se ao menos um dos limites laterais não existem, o limite da função neste ponto também não existe. 

Continue seus estudos sobre limites laterias com alguns exercícios resolvidos clicando aqui.