Limites envolvendo raiz – exercícios resolvidos de limites

Frequentemente nas listas de exercícios de limites nos deparamos com Limites envolvendo raiz, ou seja, aqueles limites em que na sua lei de formação possuem radicais, sendo os mais comuns as raízes quadradas. Em geral, os exercícios de Limites envolvendo raiz são elaborados na forma de uma divisão (razão), na qual o termo que possui a raiz pode estar tanto no numerador quanto no denominador.

Isto ocorre pois a intensão deste tipo de exercício é chegar em uma indeterminação. Assim se faz necessário a manipulação da expressão para eliminar esta indeterminação.

Exercícios resolvidos de limites

1) $\displaystyle\lim\limits_{x\rightarrow +\infty}\sqrt[3]{\frac{x^{2}-x+5}{8x^{2}+3x-2}}$

A intensão deste primeiro exercício é recordar a propriedade do limite de uma raiz, em que podemos trocar de ordem o limite com a raiz, assim temos:

$\displaystyle\lim\limits_{x\rightarrow +\infty}\sqrt[3]{\frac{x^{2}-x+5}{8x^{2}+3x-2}}=\sqrt[3]{\lim\limits_{x\rightarrow +\infty}\frac{x^{2}-x+5}{8x^{2}+3x-2}}$ .

Desta forma devemos resolver primeiro o limite e, em seguida, aplicar a raiz. Como temos uma divisão de polinômios e o limite que tende ao infinito, sugerimos aplicar técnica do termo de maior grau como:

$\displaystyle \sqrt[3]{\lim\limits_{x\rightarrow +\infty}\frac{x^{2}-x+5}{8x^{2}+3x-2}} =\sqrt[3]{\lim\limits_{x\rightarrow +\infty}\frac{x^{2}}{8x^{2}}}$ .

Em seguida devemos simplificar, onde obtém-se o limite de uma constante e, por fim, aplicar a raiz

$\displaystyle \sqrt[3]{\lim\limits_{x\rightarrow +\infty}\frac{x^{2}}{8x^{2}}}=\sqrt[3]{\lim\limits_{x\rightarrow +\infty}\frac{1}{8}}=\sqrt[3]{\frac{1}{8}}=\frac{1}{2}$ .

2) $\displaystyle\lim\limits_{x\rightarrow 4}\frac{x^{2}-16}{\sqrt{x}-2}$

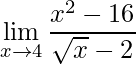
Observe que ao aplicar o limite direto obteremos uma indeterminação:

$\displaystyle\lim\limits_{x\rightarrow 4}\frac{x^{2}-16}{\sqrt{x}-2}=\frac{0}{0}$ .

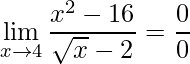Para eliminar a indeterminação aplicaremos a técnica da racionalização, que consiste em multiplicar o numerador e denominador pelo termo inverso daquele que contém a raiz

$\displaystyle\lim\limits_{x\rightarrow 4}\frac{x^{2}-16}{\sqrt{x}-2}\cdot \frac{\sqrt{x}+2}{\sqrt{x}+2}$ .

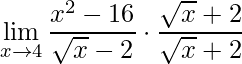Observe que no denominador temos o produto da diferença, assim obtemos:

$\displaystyle\lim\limits_{x\rightarrow 4}\frac{\left (x^{2}-16 \right )\left ( \sqrt{x}+2 \right )}{x-4}$ .

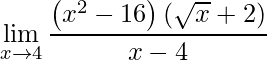Perceba que ainda não eliminamos a indeterminação, mas se abrirmos o primeiro termo do numerador no produto de suas raízes fica-se com:

$\displaystyle\lim\limits_{x\rightarrow 4}\frac{\left (x-4 \right )\left (x+4 \right )\left ( \sqrt{x}+2 \right )}{x-4}$ ,

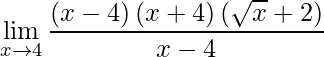na qual podemos simplificar e assim eliminar a indeterminação. Por fim, basta aplicar o limite diretamente

$\displaystyle\lim\limits_{x\rightarrow 4}\left ((x+4) ( \sqrt{x}+2) \right )=32$ .

3) $\displaystyle\lim\limits_{x\rightarrow 3}\frac{x-3}{\sqrt[3]{4-x}-1}$

Neste exercício aplica-se outra técnica muito útil em Limites envolvendo raiz, que é a mudança de variável, que consiste em um truque algébrico que facilita a solução da indeterminação da forma:

$\displaystyle\lim\limits_{x\rightarrow 3}\frac{x-3}{\sqrt[3]{4-x}-1}=\frac{0}{0}$ .

A mudança de variável para este exercício é $y=\sqrt[3]{4-x}$ e elevando ao cubo nos dois lados temos

$y^{3}=4-x$ , portanto $x=4-y^{3}$ .

Lembre que também devemos transformar o ponto limite. A partir da equação $y=\sqrt[3]{4-x}$ podemos dizer que quando $x\rightarrow 3$ temos $y\rightarrow 1$ .

Substituindo obtém-se um novo limite similar ao primeiro, que ainda contém uma indeterminação da forma:

$\displaystyle \lim\limits_{y\rightarrow 1}\frac{1-y^{3}}{y-1}=\frac{0}{0}$ .

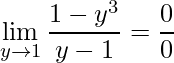Note que, desta vez podemos reescrever o limite abrindo o numerador no produto das raízes como:

$\displaystyle \lim\limits_{y\rightarrow 1}\frac{-(y-1)(y^{2}+y+1)}{(y-1)}$ ,

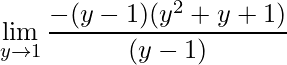simplificando e resolvendo temos

$\displaystyle \lim\limits_{y\rightarrow 1}(-y^{2}-y-1)=-3$ .

Continue seus estudos de limites assistindo a resolução de exercícios em vídeo clicando aqui.

Limites envolvendo raiz – exercícios resolvidos de limites

Baixe de forma gratuita nossos Ebooks e treinamentos

Limites envolvendo raiz – exercícios resolvidos de limites

Exercícios resolvidos de limites

1) $\displaystyle\lim\limits_{x\rightarrow +\infty}\sqrt[3]{\frac{x^{2}-x+5}{8x^{2}+3x-2}}$

2) $\displaystyle\lim\limits_{x\rightarrow 4}\frac{x^{2}-16}{\sqrt{x}-2}$

3) $\displaystyle\lim\limits_{x\rightarrow 3}\frac{x-3}{\sqrt[3]{4-x}-1}$

Compartilhe agora mesmo:

Cálculo da área de superfícies de revolução

Exemplos de Máximos e Mínimos de uma função

Volumes dos sólidos de revolução entorno do eixo y

Para enviar seu comentário, preencha os campos abaixo:

Deixe um comentário Cancelar resposta

Seja o primeiro a comentar!

Damos valor à sua privacidade

Cookies estritamente necessários

Cookies de desempenho

Cookies de funcionalidade

Cookies de publicidade

Baixe de forma gratuita nossos Ebooks e treinamentos

Limites envolvendo raiz – exercícios resolvidos de limites

Exercícios resolvidos de limites

1)

2)

3)

Compartilhe agora mesmo:

Cálculo da área de superfícies de revolução

Exemplos de Máximos e Mínimos de uma função

Volumes dos sólidos de revolução entorno do eixo y

Para enviar seu comentário, preencha os campos abaixo:

Deixe um comentário Cancelar resposta

Seja o primeiro a comentar!

Damos valor à sua privacidade

Cookies estritamente necessários

Cookies de desempenho

Cookies de funcionalidade

Cookies de publicidade

Faça aulas personalizadas sobre conteúdos específicos de Matemática e Raciocínio Lógico

1) $\displaystyle\lim\limits_{x\rightarrow +\infty}\sqrt[3]{\frac{x^{2}-x+5}{8x^{2}+3x-2}}$

2) $\displaystyle\lim\limits_{x\rightarrow 4}\frac{x^{2}-16}{\sqrt{x}-2}$

3) $\displaystyle\lim\limits_{x\rightarrow 3}\frac{x-3}{\sqrt[3]{4-x}-1}$