Demonstração das propriedades de limites – Parte II
Este é o segundo post em que estamos apresentando a Demonstração das propriedades de limites. Em geral, estas demonstrações não são feitas nas disciplinas de cálculo nos cursos engenharias e, possivelmente, nem nos de matemática, cabendo apenas às disciplinas de análise matemática. Visto que, julgamos importante para uma formação completa dos acadêmicos, daremos continuidades com a propriedade da multiplicação de limites e divisão de limites.
Para iniciar devemos lembrar da definição formal de limite, em que ![]() significa que para todo
significa que para todo ![]() existe um
existe um ![]() , tal que
, tal que
![]() implica em
implica em ![]() .
.
1) Propriedade da multiplicação de Limites
Sejam os limites ![]() e
e ![]() , então
, então
![]() .
.
Demonstração
Pela definição formal de limite temos, dado ![]() , existem
, existem ![]() e
e ![]() tais que
tais que
![]()
e
![]() .
.
Queremos mostrar que
![]() .
.
Assim, tomando ![]() , onde
, onde ![]() temos
temos
![]()
![]() .
.
Nesta última linha aplicamos a desigualdade triangular. Em seguida, basta utilizar as hipóteses dos limites de f(x) e g(x)
![]()
![]() .
.
Portanto, temos que o limite da multiplicação é equivalente à multiplicação dos limites.
2) Propriedade da divisão de Limites
Sejam os limites ![]() e
e ![]() para
para ![]() então
então
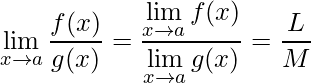 .
.
Demonstração
Como acabamos de demonstrar a propriedade do produto dos limites, podemos manipular o limite da seguinte forma
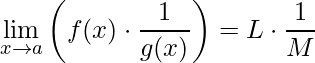 .
.
Se mostrarmos que 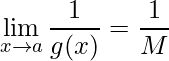 para
para ![]() , concluímos a demonstração.
, concluímos a demonstração.
Dado ![]() , existem
, existem ![]() e
e ![]() tais que
tais que
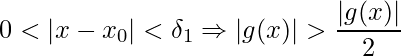
e
![]() .
.
Assim, tomando o menor valor de delta ![]() , onde
, onde ![]() , temos
, temos
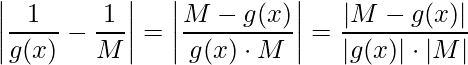
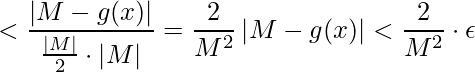 .
.
Assim concluímos as demonstrações das principais propriedades de limites. Caso você ficou animado e interessado com estas demonstrações mais formais, que na maioria das vezes não consta nas disciplinas de cálculo, recomentamos como leitura livros de Análise Matemática.
Continue seus estudos de limites observando as outras propriedades dos Limites clicando aqui, e se não viu a demonstração da propriedade do limite da soma ou da subtração clique aqui.



Deixe um comentário