Problemas de Máximos e Mínimos – Exercícios resolvidos

Dentro das aplicações da derivada nos deparamos com os Problemas de Máximos e Mínimos, que consiste em encontrar o maior e o menor valor da função em um determinado intervalo. Há um tempo atrás já publicamos um post explicando um pouco sobre os pontos de máximo e de mínimo local. Caso queira rever clique aqui.

Este post de hoje dedicaremos nossa atenção em resolver um problema prático que envolvam máximos e mínimos. Para isto utilizam-se 6 passos:

• Desenhar um esboço do problema;
• Retirar os dados fornecidos pelo exercício;
• Achar as dependências entre as variáveis;
• Encontrar a equação que relacione as variáveis a ser maximizada ou minimizada;
• Derivar e igualar a zero para obter os pontos de máximo ou mínimo.
• Analisar as condições físicas do problema.

Obs: Este último passo se aplica quando encontramos mais de um ponto de máximo ou mínimo, assim necessitamos avaliar qual dos pontos possui sentido para o problema dado.

Problemas de Máximos e Mínimos

Uma empresa de embalagem recebeu um pedido de caixas de papelão, onde o solicitante exigiu apenas que as caixas tivesse 15 litros de capacidade e uma altura de 20 centímetros. Quais são as dimensões das caixas para obter o menor custo com o papelão? (Obs: as caixas devem ser no formato de paralelepípedos reto.)

Iniciamos fazendo um esboço da caixa de papelão.

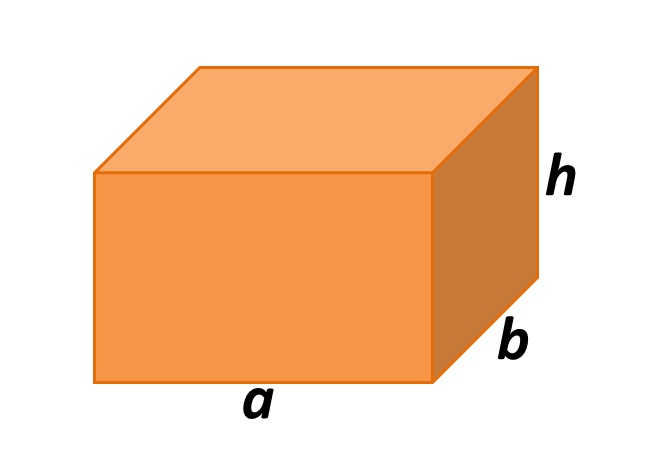
Extraindo os dados do problema: 

• Altura da caixa:
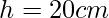
• Volume da caixa: 

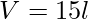
Lembre-se que devemos trabalhar sempre com as mesmas unidades de medida, assim devemos transformar litros em centímetros cúbicos, na qual

, assim  .

Em seguida, devemos encontrar as dependências entre as variáveis do problema para obter:

Volume: .

Área:  .

Observe que multiplicamos por 2, pois os lados de um paralelepípedo reto são dois-a-dois iguais.

Agora devemos encontrar a equação que relacione as variáveis a ser minimizada, pois queremos obter o menor consumo de papelão.

Pela equação do volume encontramos

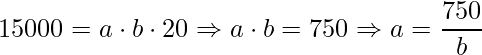
e substituindo na equação da área as informações obtemos

.

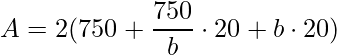
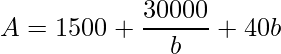Derivando em relação a variável b fica-se com

.

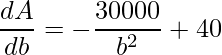Lembre-se que os pontos de máximos e mínimos são aqueles nos quais o valor da derivada é nula, ou seja, 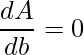. Assim, substituindo e manipulando a expressão obtém-se:

.

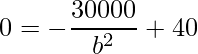
Entretanto, o valor que possui sentido físico do problema são medidas positivas, assim . Por fim, devemos encontrar a outra dimensão

 .

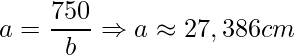Portanto, a caixa de papelão deve ter um fundo quadrado de lado aproximadamente para obter o menor consumo de papelão na sua fabricação.

Caso desejar acompanhe a resolução de outro exemplo em vídeo clicando aqui.