Aplicações das derivadas no estudo das funções

Neste post veremos uma outra aplicação do estudo das derivadas, que são as Aplicações das derivadas no estudo das funções. Com o auxilio das derivadas podemos obter mais informações sobre o comportamento das funções e assim esboçar com maior precisão o seu gráfico.   

A primeira derivada no estudo das funções

Lembre-se que a primeira derivada, dada por , nos fornece o coeficiente angular da reta tangente, assim nos pontos onde

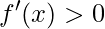• a função é crescente;
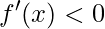• a função é decrescente;
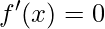• a função possui pontos de máximos ou mínimos local.

Veja este comportamento no exemplo:

Exemplo 1: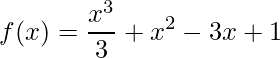 

Aplicando a derivada em uma função polinomial temos

.

Iniciamos encontrando os pontos de máximos e mínimos, que consiste em encontrar as raízes, pois devemos fazer .

Para encontrar as raízes você pode utilizar o método que preferir, eu particularmente indico o método Soma e Produto. Assim obtemos

e .

Com este resultado em mãos devemos encontrar onde a função é crescente e decrescente a partir das derivadas e .

Observe que é um problema de inequações, e , onde já resolvemos detalhadamente um exercício similar, caso queira rever clique aqui.

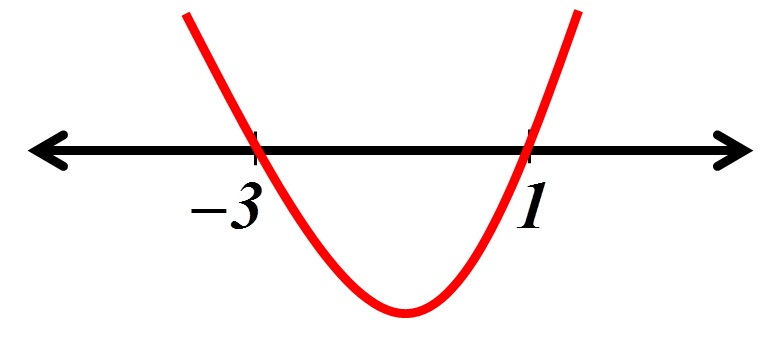
Como é uma inequação do 2º grau com concavidade para cima e já calculamos suas raízes, temos que é crescente em e decrescente em . Observe este comportamento no esboço a seguir

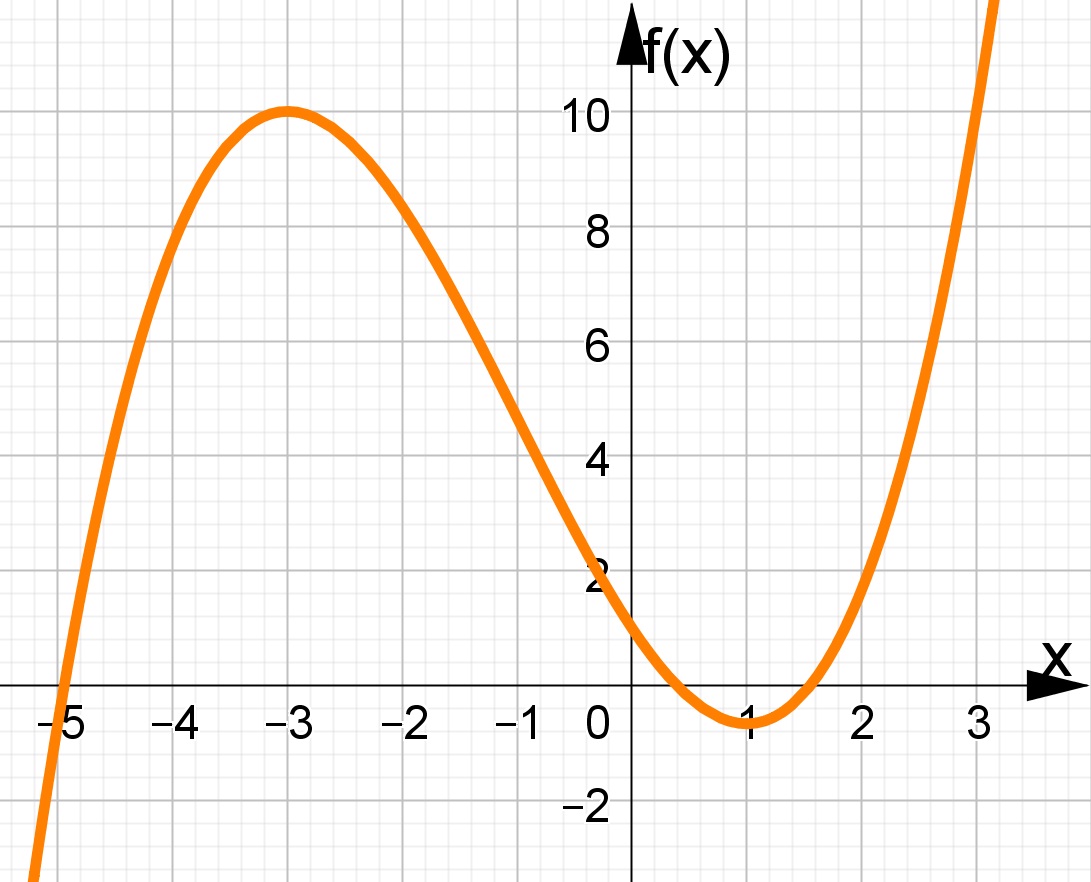
Na figura a baixo encontra-se o gráfico da função dada, onde podemos observar as caracteristicas que acabamos de analisar. 

A segunda derivada no estudo das funções

Se a função admite uma segunda derivada, , então nos pontos onde a função possuir as derivadas

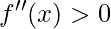• a função tem a concavidade voltada para cima;
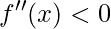• a função tem a concavidade voltada para baixo;
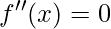• são os pontos de inflexão, ou seja, onde a função está muda o sentido da concavidade.

Veja este comportamento na mesma função do exemplo anterior:

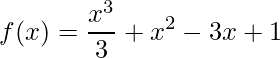
Aplicando a derivada duas vezes obtemos

.

Iniciemos calculando os pontos de inflexão, ou seja,  que são os pontos onde a função muda o sentido da concavidade.

Portanto, devemos encontrar , na qual temos 

. 

E para encontrar onde a concavidade é voltada para cima, , ou para baixo, , devemos resolver as inequações, respectivamente, 

e .

Para isto construímos o esboço do gráfico da segunda derivada 

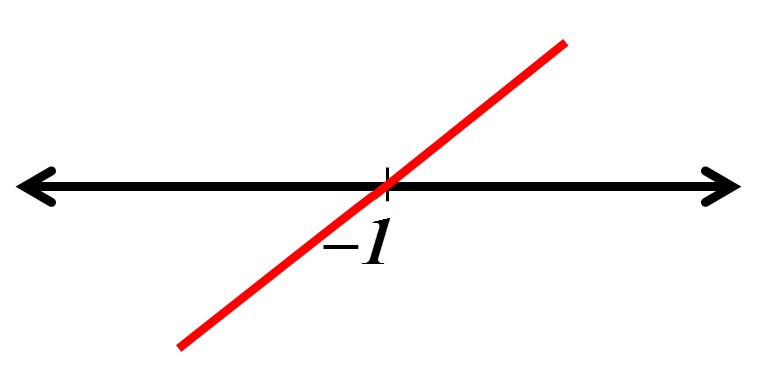
assim percebemos que ela é em o que significa que a concavidade é voltada para cima e  em o que significa que a concavidade é voltada baixo.

Acompanhe a resolução de um exercício de máximos e mínimos em vídeo clicando aqui.