Aplicações de derivadas na economia

Tanto as empresas como os governos devem estar sempre atentos as novas notícias do mercado econômico. Onde num curto espaço de tempo, deve-se tomar decisões para minimizar perdas ou maximizar lucros.  Ou também, em um processo produtivo de uma industria, o administrador deve saber a quantidade de peças produzidas que geram o menor do custo da produção. 

Para resolver ambas situações deve-se aplicar, entre outros, o conhecimento de derivadas, ou seja, o problema consiste em encontrar os pontos de máximos e mínimos. Nesta temática, o post de hoje traz algumas situações onde temos Aplicações de derivadas na economia.

Custo Marginal – Aplicações de derivadas na economia

Talvez esta seja aplicação mais conhecida de derivadas na economia, onde custo marginal pode ser definida como sendo:

• o aumento do custo provocado pela produção de mais uma unidade do produto; 
• ou ainda, custo da última unidade extra de produto produzida.

Mas não confunda Custo Marginal com Custo Médio, pois custo marginal é calculado como a variação instantânea do custo de uma unidade. Enquanto que o custo médio é dado pela média do custo total dividido pelo quantidade total de unidades produzidas. 

Matematicamente, função de custo marginal é dada pela derivada do custo total em função da quantidade total produzida: 

,

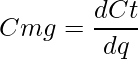onde  é o custo marginal,  é o custo total e  é a quantidade total produzida. De modo similar podemos abordar lucro marginal e receita marginal pois os princípios são os mesmos, a única alteração é a função a ser derivada.

Otimização – Aplicações de derivadas na economia

Outra aplicação muito comum é em problemas de otimização, onde estamos interessados em maximizar receitas/lucros ou minimizar custos. Tradicionalmente chamamos este tipo de aplicação de problemas de máximos ou mínimos. Pois a meta é determinar os pontos onde a função (lucro, receita, custo, …) alcança seus pontos de máximos ou mínimos.

Um exemplo prático ocorre na venda de certos produtos, onde temos a seguinte situação: caso o preço do produto for muito alto, ocorrem poucas vendas e consequentemente pouco lucro. Entretanto, caso o produto for muito barato, mesmo havendo muitas vendas, o lucro total é pequeno, pois a margem de lucro por produto vendido é pequena.

Assim, tendo em mãos a função que descreve o lucro em relação ao preço do produto e utilizando as derivadas, podemos determinar o preço ideal para obter o maior lucro possível. Entretanto, em situações reais, obter uma função que descreve exatamente a realidade é um pouco complexo, visto inúmeras variáveis envolvidas. 

Veja outras aplicações praticas das derivadas na economia com exemplos resolvidos em vídeo clicando aqui.