A regra da cadeia passo a passo
No estudo das derivadas a regra da cadeia é uma ferramenta muito importante, pois ela possibilita derivar funções mais complexas (composição de funções simples). A ideia principal desta regra é abrir essas funções complicadas na composição de funções simples em que sabemos suas derivadas. Assim, iniciamos apresentando o Teorema da regra da cadeia e, em seguida, resolvem-se alguns exemplos utilizando a Regra da cadeia passo a passo.
Teorema da regra da cadeia
Seja ![]() uma função diferenciável no ponto
uma função diferenciável no ponto ![]() e
e ![]() diferenciável no ponto
diferenciável no ponto ![]() , então a composição
, então a composição ![]() é diferenciável no ponto
é diferenciável no ponto ![]() e
e
![]() .
.
Em outras bibliografias, você pode encontrar também a regra da cadeia escrita da seguinte forma
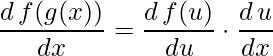 ,
,
onde ![]() , ou ainda, de forma mais simplificada
, ou ainda, de forma mais simplificada
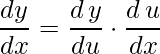 .
.
Exemplos – regra da cadeia passo a passo
1) Determine a derivada da função 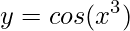 .
.
O primeiro passo é identificar a composição da função:
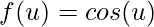 ;
;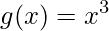 .
.
O segundo passo é derivar cada uma das funções simples separadamente:
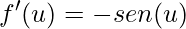 ;
;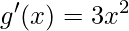 .
.
O terceiro passo é substituirmos na fórmula da regra da cadeia:
![]() .
.
Por fim, substituir a função auxiliar ![]() e simplificar a solução
e simplificar a solução
![]()
![]() .
.
2) Determine a derivada da função ![Rendered by QuickLaTeX.com \displaystyle y=ln(\sqrt[3]{e^{x}+1})](https://dicasdecalculo.net/wp-content/ql-cache/quicklatex.com-8fb3953d181ba85c00a4559abbcc80a6_l3.png) .
.
Observe que essa função é formada pela composição de 3 funções simples. Assim, devemos aplicar a regra da cadeia duas vezes.
O primeiro passo é identificar a composição das funções simples:
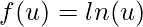 ;
;![Rendered by QuickLaTeX.com \displaystyle g(v)=\sqrt[3]{v}](https://dicasdecalculo.net/wp-content/ql-cache/quicklatex.com-670b033431ec30edd7d404bcf3a63862_l3.png) ;
;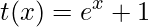 .
.
onde ![]() e
e ![]() .
.
O segundo passo é derivar cada uma das funções simples separadamente:
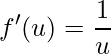 ;
;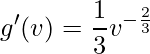 ;
;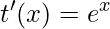 .
.
O terceiro passo é substituirmos na fórmula da regra da cadeia:
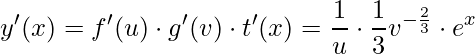 .
.
Por fim, substituir as funções auxiliar ![]() ,
, ![]() e simplificar a solução
e simplificar a solução
![Rendered by QuickLaTeX.com \displaystyle y'(x)=\frac{1}{\sqrt[3]{v}}\cdot \frac{1}{3}(e^{x}+1)^{-\frac{2}{3}}\cdot e^{x}](https://dicasdecalculo.net/wp-content/ql-cache/quicklatex.com-62edc1b7cd2f08191bbd13f57d207dae_l3.png)
![Rendered by QuickLaTeX.com \displaystyle y'(x)=\frac{1}{\sqrt[3]{e^{x}+1}}\cdot \frac{1}{3}(e^{x}+1)^{-\frac{2}{3}}\cdot e^{x}](https://dicasdecalculo.net/wp-content/ql-cache/quicklatex.com-c716240c6ae700d1c652b06bff20b465_l3.png)
![Rendered by QuickLaTeX.com \displaystyle y'(x)=\frac{1}{\sqrt[3]{e^{x}+1}}\cdot \frac{1}{3\sqrt[3]{(e^{x}+1)^{2}}}\cdot e^{x}](https://dicasdecalculo.net/wp-content/ql-cache/quicklatex.com-9690d18d9b9ae7eebd2b0c7ac6e3a2c7_l3.png)
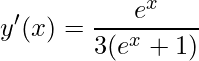 .
.
Acompanhe a resolução de outros exercícios que utilizam a Regra da Cadeia clicando aqui.



Deixe um comentário