Regra de L’Hospital definição e exemplos resolvidos
Em muitos cálculos de limites nos deparamos com um dos tipos de indeterminação. Assim temos que aplicar alguma técnica para superar esta indeterminação, como por exemplo a fatoração. Entretanto há casos em que não é possível aplicar estas técnicas. Nesses casos devemos recorrer a Regra de L’Hospital, que foi desenvolvida por Bernoulli, entretanto publicada por L’Hospital. Bernoulli percebeu que na vizinhança de um determinado ponto, a razão entre duas funções pode ser comparada com a razão entre suas derivadas, desde que sejam atendidas algumas hipóteses.
Regra de L’Hospital definição
Sejam ![]() e
e ![]() duas funções contínuas e deriváveis em um intervalo
duas funções contínuas e deriváveis em um intervalo ![]() , com
, com ![]() em todo
em todo ![]() . Se
. Se
![]() ou
ou ![]()
e se existe 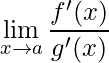 finito ou infinito então
finito ou infinito então
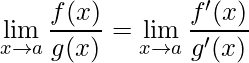 .
.
Observação: O mesmo vale se ![]() for substituído por
for substituído por ![]() ,
, ![]() ,
, ![]() ou
ou ![]() .
.
Exemplos resolvidos
Determine os limites que seguem:
1)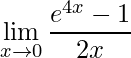
O cálculo direto do limite nos dá a forma indeterminada 0/0.
Perceba que as hipóteses necessárias para a aplicação da regra de L’Hospital são satisfeitas .
Então devemos derivar numerador e denominador separadamente, onde obtermos o limite desejado
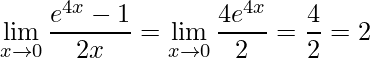 .
.
O caso você tenha dificuldade na derivação, clique aqui e acompanhe a resolução de alguns exemplos passo a passo.
2) 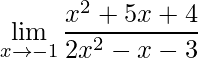
O cálculo direto do limite nos dá a forma indeterminada 0/0.
Este exercício é formado por polinômios, então poderíamos aplicar a fatoração nas raízes dele, onde encontraríamos
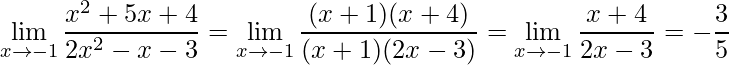 .
.
Entretanto perceba como é muito mais fácil e rápido aplicar a regra de L’Hospital, em que devemos apenas derivar e aplicar o ponto limite
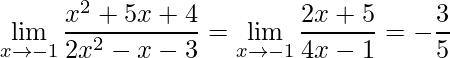 .
.
3) 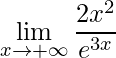
O cálculo direto do limite nos dá a forma indeterminada ![]() .
.
Novamente as hipóteses da regra de L’Hospital são satisfeita, assim derivando temos
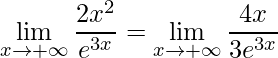 .
.
Observe que temos uma nova indeterminada ![]() . Assim podemos aplicar uma nova vez L’Hospital, visto que as hipóteses ainda são satisfeita
. Assim podemos aplicar uma nova vez L’Hospital, visto que as hipóteses ainda são satisfeita
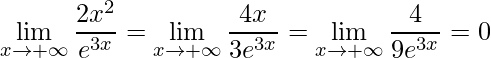 .
.
Observação: Podemos aplicar quantas vezes forem necessárias as regra de L’Hospital, desde que as hipóteses sejam satisfeitas.
Acompanhe também explicações e resoluções de outros exemplos em vídeo, clicando aqui.



Deixe um comentário