Concavidade de uma função e exemplos resolvidos 

O estudo da concavidade de uma função nos auxilia a compreender melhor o comportamento do seu gráfico. Como já vimos em posts anteriores, a primeira derivada nos aponta onde a função é crescente ou decrescente, porém não nos revela a sua curvatura.

Por exemplo, na figura a seguir temos a função cúbica que é sempre crescente, entretanto seu comportamento é diferente em x>0 e x<0. Observe

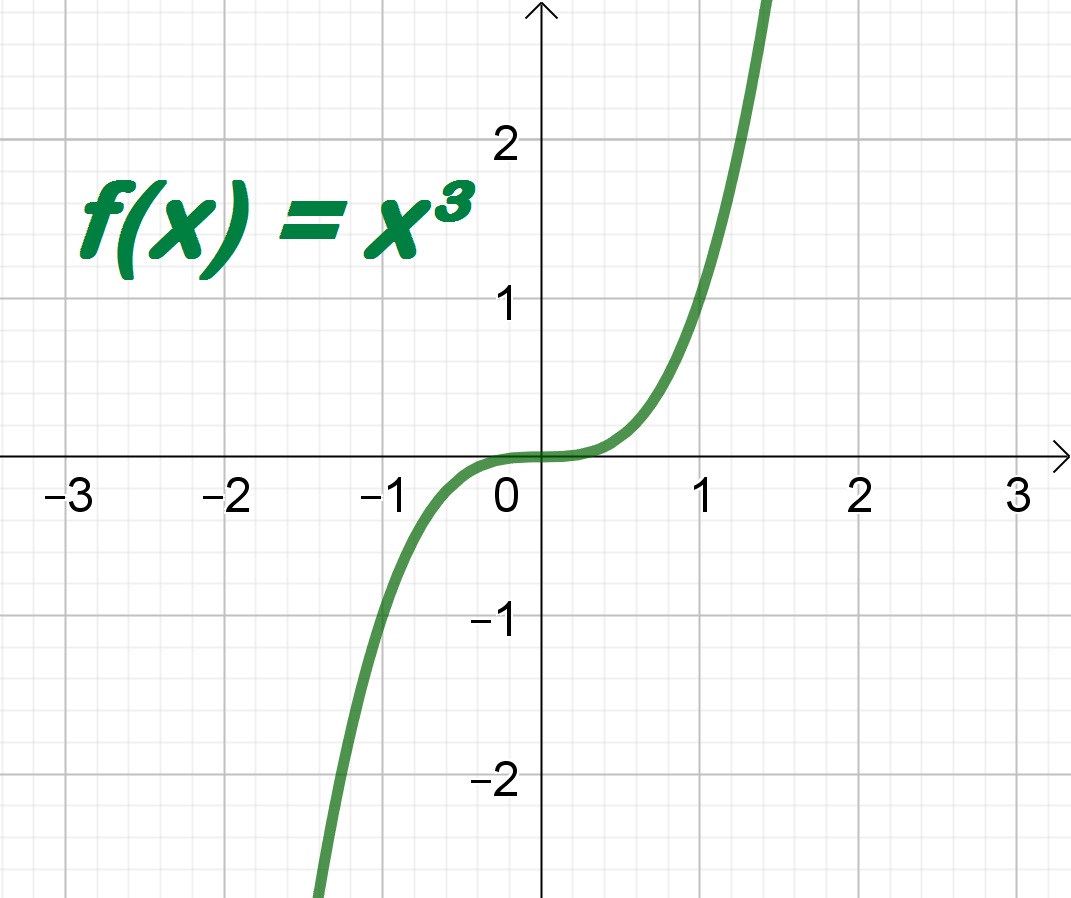
Desta forma, saber determinar onde a função possui concavidade para cima ou para baixo nos possibilita traçar o gráfico com maior exatidão. 

Teorema da concavidade das funções 

Seja a função duas vezes diferenciável em uma intervalo aberto I, então dizemos que

• A função 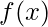 tem concavidade para cima no intervalo I se ;
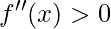• A função 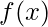 tem concavidade para baixo no intervalo I se .

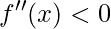Exemplo Resolvido

1) Analise o comportamento da concavidade da função  .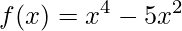 

Neste exemplo temos a função polinomial de quarta ordem. Ao derivar pela primeira vez temos:

. 

Em seguida, derivando mais uma vez temos

.

Agora devemos analisar o comportamento desta segunda derivada, ou seja, determinar onde   e .

Para isto devemos utilizar as inequações e determinar os intervalos de cada uma delas. Caso você tenha dificuldade em resolver este tipo de inequação, clique aqui onde já resolvemos um exemplo de Inequação do 2º Grau. Separando em dois casos:

Neste caso temos como intervalo  .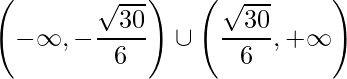

Obs: .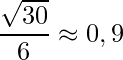

Neste outro caso temos  .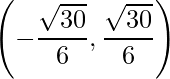

Na figura a baixo podemos ver claramente o comportamento em que determinados a partir do estudo da segunda derivada.

Obs: nos pontos onde função não possui concavidade para cima ou para baixo sao conhecidos como pontos de inflexão, ou seja, onde .

Acompanhe também explicações e resoluções de outros exemplos em vídeo, clicando aqui.