Resolvendo derivadas usando a definição
Costumeiramente, inicia-se o estudo das derivadas Resolvendo derivadas usando a definição, ou seja, derivar uma função via limite. Este limite significa tornar uma reta secante do gráfico da função em uma reta tangente em um determinado ponto desta curva, mais detalhes clique aqui.
Relembrando a Definição
Uma função ![]() definida em um intervalo aberto
definida em um intervalo aberto ![]() é derivável em
é derivável em ![]() se existir o seguinte limite
se existir o seguinte limite
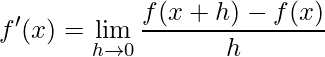 ,
,
onde ![]() representa a derivada de
representa a derivada de ![]() .
.
Exercícios resolvidos
Resolvendo derivadas usando a definição:
1)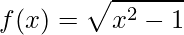
Iniciamos aplicando a definição de derivadas na função f(x), onde na variável x devemos aplicar (x+h) e tomarmos a limite de h tendendo a 0. Assim, temos
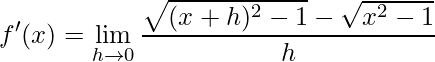 .
.
A partir deste momento, o que temos para resolver é o cálculo de um limite, neste caso temos uma função racional com a presença de raízes. No post passado já resolvemos um exercício semelhante. O artifício que usamos foi a racionalização do numerador, visto que a aplicação direta do limite obtermos uma indeterminação.
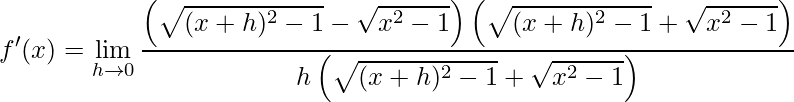 .
.
Multiplicando o numerado, perceba que temos um produto notável: Produto da Soma pela Diferença, assim temos apenas o quadrado do primeiro termo menos o quadrado do segundo termo
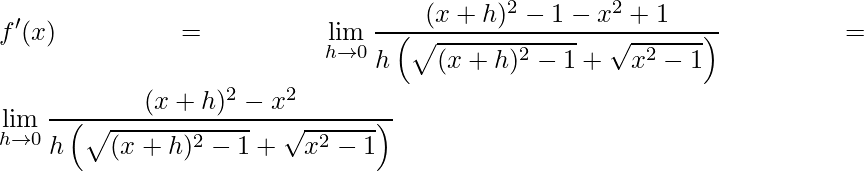 .
.
Abrindo o termo ao quadrado do numerado e fazendo as simplificações necessárias obtemos
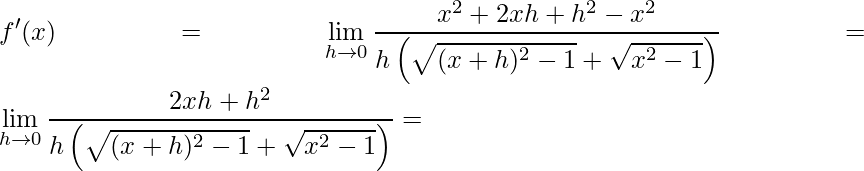
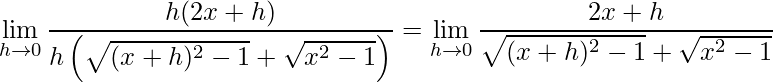 .
.
Agora aplicando o limite, somando os termos do denominador e fazendo uma última simplificação chega-se ao resultado desejado
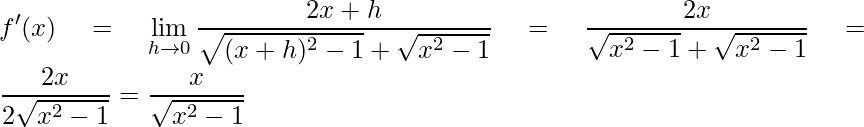 .
.
2)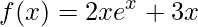
Aplicando a definição de derivada na função dada obtemos
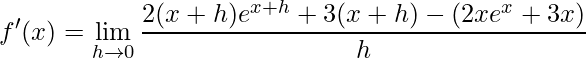
em seguida, aplicando as propriedades da exponencial e fazendo algumas simplificações
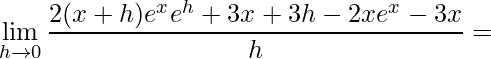
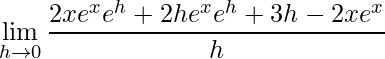 .
.
O próximo passo é agrupar os termos que possuem x e os termos que possuem h
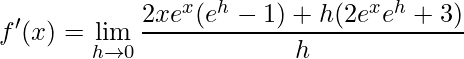
em seguida, aplicamos a Propriedade da Soma de Limites, assim obtemos
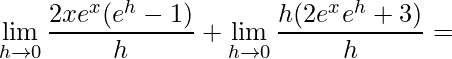
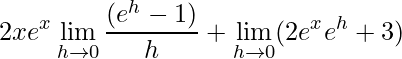 .
.
Perceba que o primeiro limite é um Limite Fundamental e o segundo podemos aplicar o limite direto, assim temos
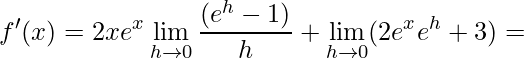
![]() .
.
Logo, chega-se ao resultado que buscávamos
![]() .
.
Acompanhe também explicações e resoluções de outros exemplos em vídeo, clicando aqui.


Deixe um comentário