Regra da Cadeia passo a passo – Resolvendo Derivadas
Neste post apresentaremos a Regra da Cadeia passo a passo, esta que é uma das várias regras/propriedades das derivadas, que nos permite determinar as derivadas das funções sem o usar a definição. Esta regra de derivação é aplicada em funções compostas, ou também chamadas de funções de funções, onde uma função f(x) é o domínio da função g(u) sendo u=f(x), ou seja, g[f(x)].
Entretanto para podermos utilizar a temos Regra da Cadeia, as funções f(x) e g(u) devem ser deriváveis. Assim, antes aplicarmos a Regra da Cadeia passo a passo, devemos relembrar o seu Teorema:
Se ![]() for diferenciável no domínio
for diferenciável no domínio ![]() e
e ![]() for diferenciável no domínio
for diferenciável no domínio ![]() , então a função composta
, então a função composta ![]() (também escrita como
(também escrita como ![]() ) é diferenciável em
) é diferenciável em ![]() . Além disso, a derivada é dada por
. Além disso, a derivada é dada por
![Rendered by QuickLaTeX.com \displaystyle \frac{d}{dx}\bigg[g\big(f(x)\big)\bigg]=\frac{d}{du}\big[g(u)\big]\cdot \frac{d}{dx}\big[f(x)\big]](https://dicasdecalculo.net/wp-content/ql-cache/quicklatex.com-ab8219fe808f85eeb2fdbea25b2944f9_l3.png) ,
,
onde ![]() .
.
Exercícios resolvidos
Derive as seguintes funções usando a Regra da Cadeia:
1)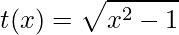
O primeiro passo para derivarmos funções compostas é identificar a composição da função dada, ou seja, o que representa a função ![]() e o que representa a função
e o que representa a função ![]() , neste caso temos
, neste caso temos
,
.
O próximo passo é derivar ambas funções separadamente, uma agora dependendo de x e a outra dependendo de u. Observe que nas duas podemos utilizar Derivada da Potência, uma vez que temos uma função raiz básica. Assim temos
,
.
O último passo é substituir na fórmula da Regra da Cadeia, lembrando que ![]() assim temos
assim temos
![Rendered by QuickLaTeX.com \displaystyle \frac{d}{dx}\bigg[t(x)\bigg]=\frac{d}{dx}\bigg[g\big(f(x)\big)\bigg]=\frac{d}{du}\big[g(u)\big]\cdot \frac{d}{dx}\big[f(x)\big]=\frac{1}{2\sqrt{u}}\cdot 2x=](https://dicasdecalculo.net/wp-content/ql-cache/quicklatex.com-a6dd37659815aa46db6144fa72bb74dc_l3.png)
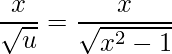 .
.
2)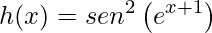
Novamente, o primeiro passo para derivarmos funções compostas é identificar a composição da função dada. Observe que essa função é formada pela composição de 4 funções simples. Assim, devemos aplicar a regra da cadeia três vezes.
onde
;
onde
;
onde
;
.
O segundo passo é derivar todas funções separadamente, aqui utilizamos a derivada da potência, derivada trigonométrica, derivada exponencial e derivada da potência, respectivamente, caso tenha dificuldade em alguma delas clique aqui,
;
;
;
.
O terceiro passo é substituirmos na fórmula da regra da cadeia, como temos três composições, a regra da cadeia resultante ficará da seguinte forma
![]()
onde ![Rendered by QuickLaTeX.com \displaystyle h'(x)=\frac{d}{dx}\big[h(x)\big]](https://dicasdecalculo.net/wp-content/ql-cache/quicklatex.com-6e6adf5f70c1a79d26ae2c5b05fd98a2_l3.png) . Assim
. Assim
![]() .
.
O último passo é substituir as funções u, v e w para obter a derivada desejada
![]()
Acompanhe também explicações e resoluções de outros exemplos em vídeo, clicando aqui.



Deixe um comentário