Integração por Substituição passo a passo – Resolvendo Integrais
Neste post resolveremos algumas integrais utilizando a Integração por Substituição passo a passo. Lembrando que recentemente publicamos uma ideia inicial da Integração por Substituição, como sendo a antiderivada da Regra da cadeia. Para ficar mais clara a sua aplicação, dedicaremos este post a resolver alguns exemplos passo a passo buscando eliminar possíveis dúvidas.
Dica: se você ao observar uma integral perceber que o integrando pode ser separado em dois termos e que a derivada de um deles é semelhante ao outro, possivelmente a metodologia a ser utilizada é a Integração por Substituição.
Obs: lembre-se que ao fazer a substituição, a variável do problema original não deve mais aparecer na nova integral. Ou seja, devemos ter apenas a variável que tivermos proposto para a substituição, em geral, utilizamos a substituição de uma função de x para um função em u.
Exercícios resolvidos de Integração por Substituição passo a passo
1)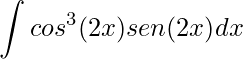
Neste exercício podemos perceber facilmente o que dissemos na dica, pois a derivada
![Rendered by QuickLaTeX.com \displaystyle \frac{d}{dx}\bigg[cos(2x)\bigg]=-2sen(2x)](https://dicasdecalculo.net/wp-content/ql-cache/quicklatex.com-e2915baf28b0366fccaab1f439fbb744_l3.png)
é semelhante do outro termo do integrando. Assim, quando substituímos ![]() e derivando ambos os lados
e derivando ambos os lados
![Rendered by QuickLaTeX.com \displaystyle \frac{du}{dx}=\frac{d}{dx}\bigg[cos(2x)\bigg]=-2sen(2x)](https://dicasdecalculo.net/wp-content/ql-cache/quicklatex.com-fc1eda47334d0d95e622b5d5500f6bc4_l3.png)
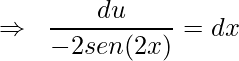 .
.
Substituindo na integral original obtém-se
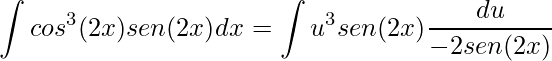
e simplificando chega-se a uma integral imediata em que sabemos sua integral
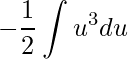 .
.
Ao aplicar a integral imediata teremos
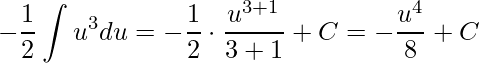 .
.
Por fim, substituindo a expressão referente a u chega-se a solução da integral
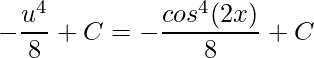 .
.
Portanto,
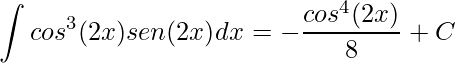 .
.
2)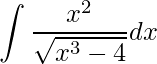
Novamente, o primeiro passo é determinar qual termo que derivado possui mesma estrutura dos demais, que podemos simplificar ou substituir a fim de eliminar a variável x.
Neste caso, perceba que se derivarmos a função que está no radicando (dentro da raiz), obteremos uma função semelhante da função do numerador. Assim, ao fazer a substituição eliminaremos a variável x. Tomando ![]() e derivando ambos os lados
e derivando ambos os lados
![Rendered by QuickLaTeX.com \displaystyle \frac{du}{dx}=\frac{d}{dx}\bigg[x^{3}-4\bigg]=3x^{2}](https://dicasdecalculo.net/wp-content/ql-cache/quicklatex.com-a6bfba2dadbb55ce7641ffc10bbc96a5_l3.png) ,
,
logo
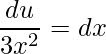 .
.
O próximo passo é substituir na integral dada a expressão u e dx, onde teremos
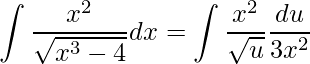 .
.
Simplificando chega-se a uma nova integral, agora na variável u. Manipularemos a integral para obtermos uma integral de função potência da forma
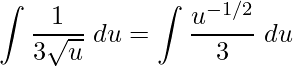 .
.
Assim, temos uma integral imediata que é dada por
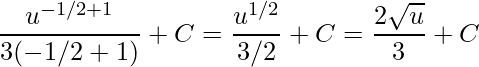 .
.
Por fim, substituindo a variável u obteremos a integral desejada
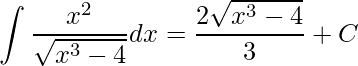 .
.



Deixe um comentário