Integrais definidas resolvidas: determinando a área através das integrais
Dedicaremos este post para as Integrais definidas resolvidas, ou seja, para determinar a área sob determinadas curvas através das integrais. Para tal, utilizaremos as Propriedades das Integrais, que publicamos recentemente e a técnica da Integração por Substituição. Caso fique alguma dúvida deixe seu comentário no final deste post.
Exercício: Integrais definidas resolvidas
Calcule a seguinte integral: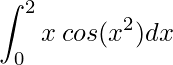
O primeiro passo para resolvermos uma integral definida é analisar o comportamento da função que está no integrando, pois se a função ora é positiva ora negativa, devemos separar em intervalos com mesmo sinal usando a 6ª propriedade das Integrais.
Para resolver este exercício, vamos supor que estamos em uma prova e que não temos o auxilio de um programa para gerar o gráfico da função dada. Assim, precisamos determinar o domínio onde ela é positiva e onde ela é negativa.
Primeiramente, perceba que é uma função contínua, pois é composta por funções polinomiais e a função cosseno. O próximo passo é localizar os zeros da função, pois nestes pontos a função pode trocar de sinal. Assim, temos que resolver
![]()
para o domínio ![]() . Em x=0 é um dos pontos, pois
. Em x=0 é um dos pontos, pois ![]() . Os demais pontos serão onde
. Os demais pontos serão onde ![]() . Sabemos que a função cosseno é igual a zero em
. Sabemos que a função cosseno é igual a zero em 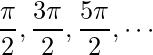 , logo:
, logo:
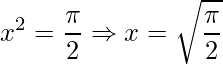 ;
;
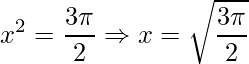 ;
;
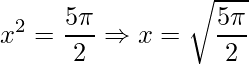 ;
;
![]() .
.
Note que destes pontos apenas 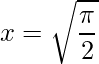 fica dentro do intervalo de integração.
fica dentro do intervalo de integração.
O próximo passo é determinar o sinal da função em cada um destes intervalos
Em 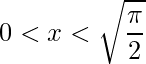 é positivo, pois
é positivo, pois ![]() e
e ![]() . Já em
. Já em 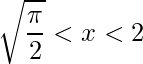 é negativo, pois
é negativo, pois ![]() e
e ![]() . Assim, temos que resolver a seguinte integral:
. Assim, temos que resolver a seguinte integral:
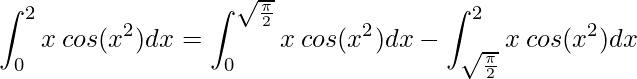 .
.
Observe que a integral onde a função é negativo temos que multiplicar por -1, pois ao integrar obteremos um valor de área negativo.
Calculo da integral de x cos(x^2)
Perceba que não temos uma integral imediata, assim utilizaremos a técnica da Integração por substituição, visto que a derivada de ![]() é semelhante a função x. Assim, tomando
é semelhante a função x. Assim, tomando ![]() e derivando teremos
e derivando teremos ![]() . Ao substituir na integral dada tem-se:
. Ao substituir na integral dada tem-se:
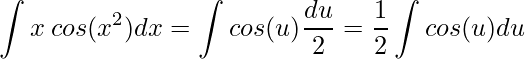 .
.
Perceba que na última igualdade utilizamos a 1ª propriedade das Integrais. Agora aplicando a integral do cosseno temos
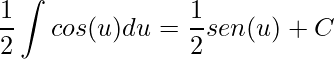
e substituindo ![]() para voltar na variável x
para voltar na variável x
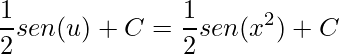 .
.
Aplicando na integral definida, lembrando que podemos omitir a constante C, teremos
![Rendered by QuickLaTeX.com \displaystyle \int^{\sqrt{\frac{\pi }{2}}}_{0} x\:cos(x^{2})dx-\int^{2}_{\sqrt{\frac{\pi }{2}}} x\:cos(x^{2})dx=\bigg[\frac{1}{2}sen(x^{2})\bigg]\bigg|^{\sqrt{\frac{\pi }{2}}}_{0}-\bigg[\frac{1}{2}sen(x^{2})\bigg]\bigg|_{\sqrt{\frac{\pi }{2}}}^{2}=](https://dicasdecalculo.net/wp-content/ql-cache/quicklatex.com-0c7c76c9d38ca08b4acdba32a1f02152_l3.png)
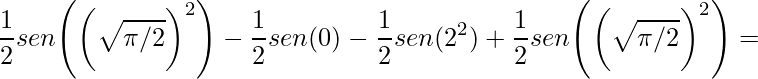
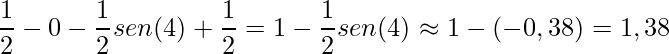 .
.
Logo,
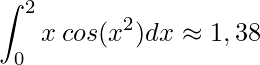 .
.
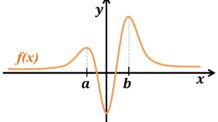
Apenas com a intenção de exemplificar, no gráfico a seguir podemos perceber o comportamento da função, como já tínhamos calculado anteriormente.
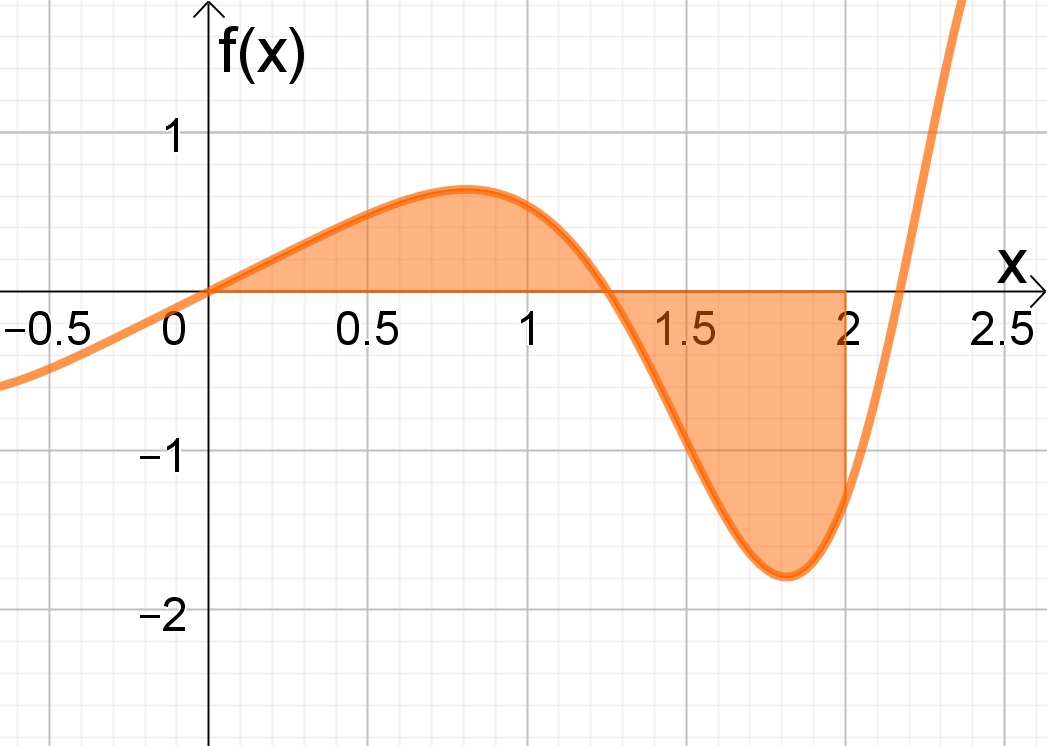



Deixe um comentário