Integração por partes: exercícios resolvidos de integrais
Após apresentarmos a técnica da Integração por partes, queremos resolver alguns exercícios passo a passo. Relembrando que esta técnica é indicada para resolver integrais que em seu integrando é formado pelo produto de funções. Onde, uma parte deve ser derivada e outra integrada, afim de reduzir a complexidade da integral original. Resolveremos cada integral detalhando cada passo, entretanto, se mesmo assim ficar alguma dúvida, deixe seu comentário no fim desta página.
Exercícios resolvidos utilizando Integração por partes
Calcule as seguintes integrais:
1) 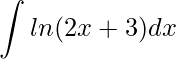
Primeiramente, lembre que funções logarítmicas não possuem integrais direta, e também, à primeira vista, não parecem ser produto de funções. Entretanto, a segunda função está camuflada, pois ela é o elemento neutro da multiplicação, ou seja, a constante 1. Veja agora, identificando este elemento
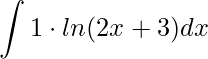 .
.
O primeiro passo para utilizarmos a Integração por partes é definirmos as funções u(x) e dv. Como não sabemos a integral de ln(2x+3), escolheremos ela para u(x). Assim,
![]() que implica em
que implica em 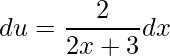 .
.
![]() que implica em
que implica em ![]() .
.
Aplicando a técnica da Integração por partes temos
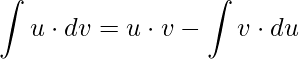 .
.
Substituindo,
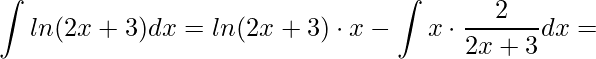
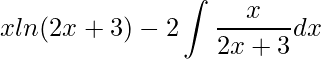 .
.
O problema da integral da função logarítmica foi superada. Entretanto, ainda temos uma integral para resolver, para ela utilizaremos a técnica da Integração por substituição. Tomando ![]() , derivando
, derivando 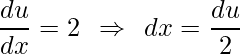 e isolando a variável x
e isolando a variável x 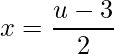 . Substituindo teremos
. Substituindo teremos
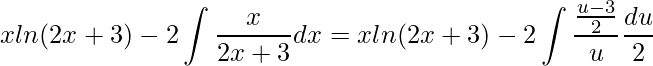 .
.
Simplificando e manipulando a expressão temos
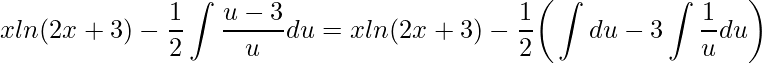 .
.
Perceba que agora temos duas integrais diretas, onde resolvendo-as teremos
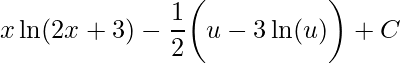 .
.
Agora só nos falta substituir a variável u por x, assim
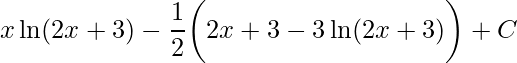 .
.
Assim temos
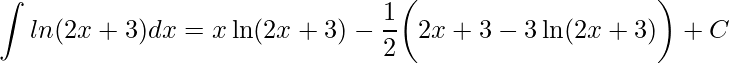 .
.
Perceba que ainda podemos manipular a solução para obter uma forma mais simplificada, contudo, isto não é obrigatório
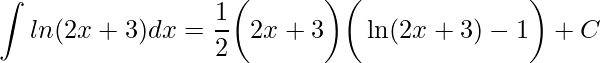 .
.
2) 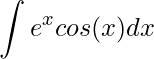
Neste segundo exercício, mais do que saber utilizar a técnica da Integração por partes, precisamos ter um insight. Ou seja, precisamos ter um sensibilidade para perceber que dentro da resolução aparecerá novamente a integral original. Aparentemente, ao aplicar a técnica da Integração por partes neste tipo de questão, estamos andando em circulo. Entretanto, é justamente isto que resolverá a integral.
Para não tornar este post muito longo, apresentaremos a resolução desta integral na próxima publicação.





Deixe um comentário