Resolvendo Integral exp(x)cos(x) usando Integração por partes

No post anterior resolvemos 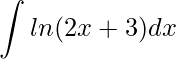, como prometido, daremos continuidade Resolvendo Integral exp(x)cos(x). Neste exercício, mais do que saber utilizar a técnica da Integração por partes, precisamos ter um insight. Ou seja, precisamos ter um sensibilidade para perceber que dentro da resolução aparecerá novamente a integral original. Aparentemente, ao aplicar a técnica da Integração por partes neste tipo de questão, estamos andando em circulo. Entretanto, é justamente isto que resolverá a integral.

Resolva: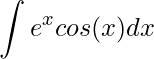

O primeiro passo para utilizarmos a Integração por partes é definirmos as funções u(x) e dv. Nesta integral é indiferente a escolha, nós optaremos u(x)=exp(x) e dv=cos(x)dx. Entretanto, você poderá escolher ao contrário e seguir os mesmos passos de resolução. Assim,

que implica em .

que implica em .

Aplicando a técnica da Integração por partes temos

.

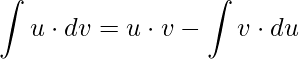Substituindo,

.

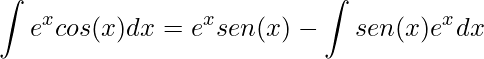Perceba que após aplicarmos a Integração por Partes, aparentemente, não resolvemos nada. Pois, permanecemos com uma integral que é formada por uma função exponencial vezes uma trigonométrica. Entretanto, estamos no caminho certo.

Como ainda temos uma integral no lado direito, devemos aplicar novamente a Integração por partes. Neste exercício é indiferente a escolha das funções u(x) e dv, note que grifei que neste exercício, pois na sua maioria a escolha influenciará na resolução. Assim,  

que implica em .

que implica em .

Substituindo os termos encontrados na fórmula da técnica da Integração por partes, temos

.

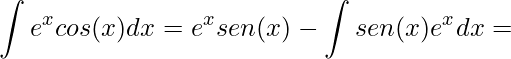
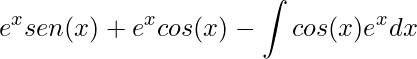Organizando a expressão toda, temos

.

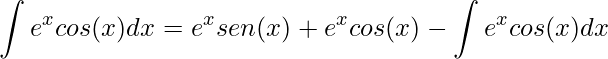Observe que a integral do termo da direito é igual a integral da esquerda, assim, isolando as duas no lado esquerdo, teremos

.

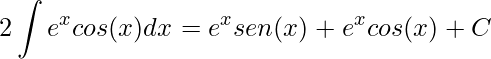Por fim, dividindo ambos os lados por 2, obtemos o resultado desejado

.

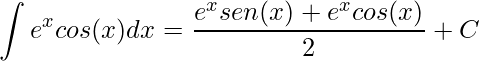Obs: como já escrevi em posts anteriores, note que coloquei a constante C apenas no fim, quando não tinhamos mais uma integral no lado direito. Visto que, cada integral produz uma nova constante.