Integrais por Substituição Trigonométrica – Exercícios resolvidos
Hoje daremos continuidade ao post da Integração por Substituição Trigonométrica, resolvendo algumas Integrais por Substituição Trigonométrica. Entretanto, se você ainda não estudou os 3 tipos possíveis de substituição, aconselho dar uma olhadinha no link acima. Como prometido, resolveremos os exercícios que envolvem os dois últimos tipos de substituição.
Resolvendo de Integrais por Substituição Trigonométrica
Resolva as seguintes integrais:
1)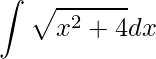
Primeiramente, devemos identificar qual dos tipos de relações que devemos utilizar para a substituição. Neste caso, o termo raiz é a soma de 2 quadrados, assim, a raiz está na hipotenusa do triângulo, logo temos o segundo tipo.
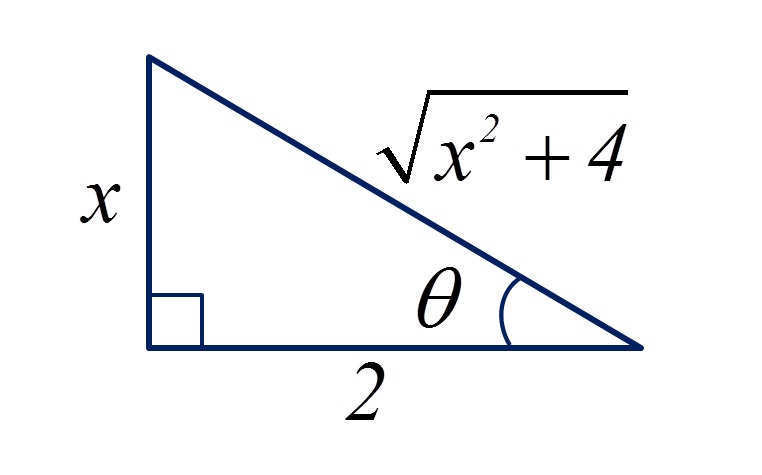
Dessa forma, podemos tirar das relações do triângulo as seguintes expressões:
- Função tangente:
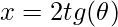 .
. - Derivada da tangente:
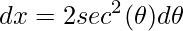 .
. - Função secante:
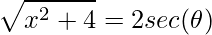 .
.
Obs: para fazer a substituição trigonométrica sempre precisamos das duas últimas expressões para substituir: o termo dx e a raiz, algumas vezes utilizamos também a variável x.
Desse modo, substituindo cada expressão na integral original teremos
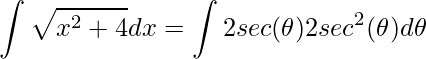 .
.
Ou seja, a nova integral
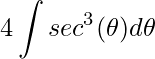 .
.
A integral de potências da função secante são encontradas em formulários presentes em muitos livros. Entretanto, resolveremos aqui passo a passo. Para isto, devemos utilizar Integração por Partes onde
![]()
![]() .
.
![]() .
.
![]() .
.
Assim, temos
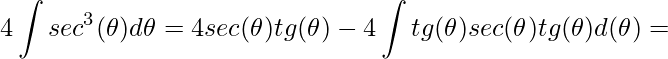
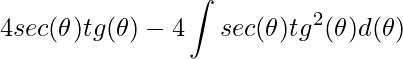 .
.
Lembre que ![]() , substituindo e organizando os termos obtemos
, substituindo e organizando os termos obtemos
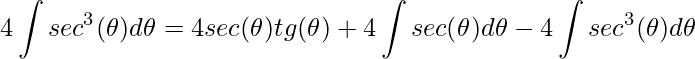 .
.
Observe que a integral do lado direito é igual a do lado esquerdo, assim, isolando e dividindo teremos
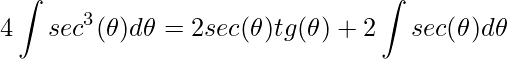 .
.
Como 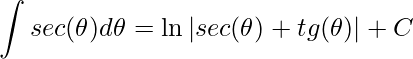 , temos
, temos
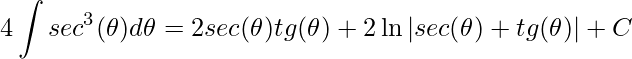 .
.
Por fim, devemos retornar a variável original, x, substituindo cada termo
- Função tangente:
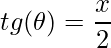 .
. - Função secante:
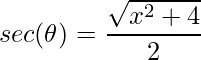 .
.
Portanto,
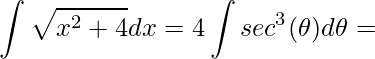
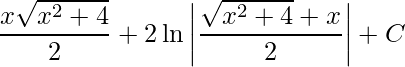 .
.
2)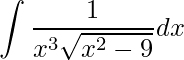
Não temos a necessidade de desenhar o triângulo para descrevermos as expressões, mas pode nos auxiliar a visualizar.
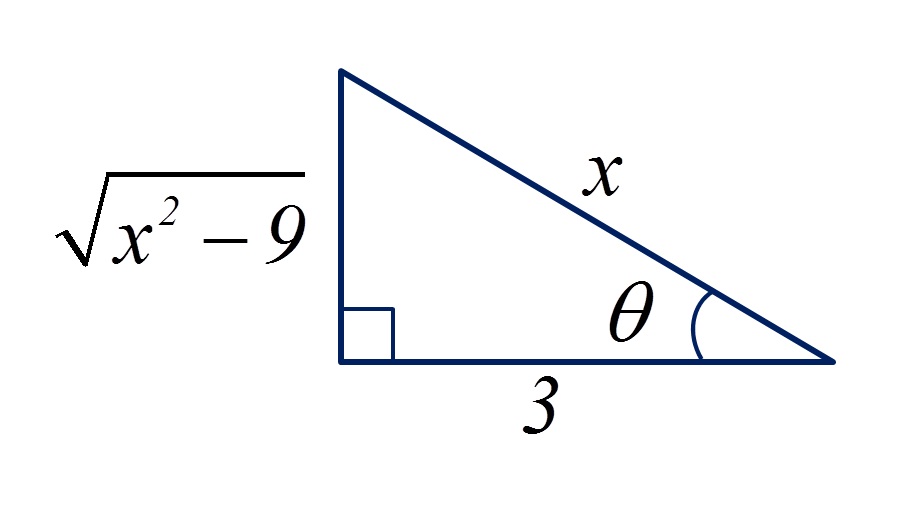
Assim temos:
- Função secante:
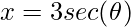 .
. - Derivada da secante:
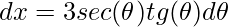 .
. - Função tangente:
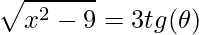 .
. 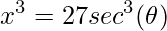 .
.
Substituindo,
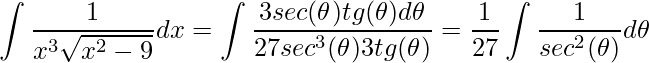 .
.
Lembre que a função secante é 1 sobre cosseno e 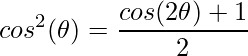 , assim
, assim
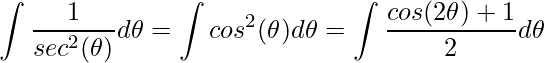 .
.
Abrindo em duas integrais e usando Integração por Substituição na integral que contém a função cosseno, obtemos
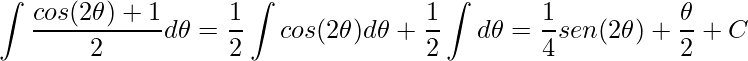 .
.
Dessa forma temos
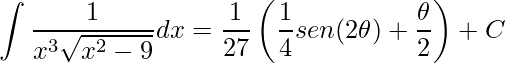 .
.
Lembrando que ![]() temos
temos
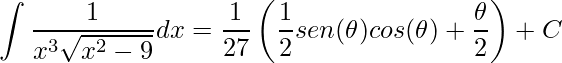 .
.
Por fim, devemos retornar a variável original, x, substituindo cada termo
- Função seno:
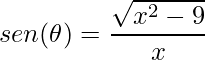 .
. - Função cosseno:
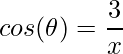 .
. - Função arcoseno:
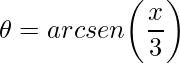 .
.
obtemos
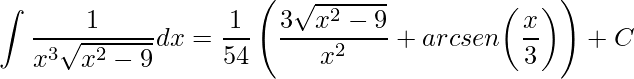 .
.



Deixe um comentário