Cálculo do volume dos sólidos de revolução – exercícios resolvidos

Neste post apresentaremos alguns exemplos do Cálculo do volume dos sólidos de revolução. Lembrando que já publicamos de forma resumida a construção da fórmula em que calcula o volume dos sólidos de revolução. Assim, nos dedicaremos hoje apenas na sua aplicação.

Primeiramente recorde que a fórmula do volume dos sólidos de revolução é dada por

$\displaystyle V=\int_{a}^{b}\pi \big(f(x)\big)^{2}dx$ .

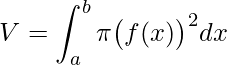onde o volume está dentro do objeto gerado ao girarmos f(x) entorno do eixo x e x=a e x=b.

Determine o volume do objeto gerado ao girarmos a\as função\funções entorno do eixo dado no domínio indicado.

1) $\displaystyle f(x)=\sqrt{4-x^{2}}$ entorno do eixo x com $\displaystyle 0\leq x\leq 2$

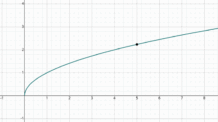
Primeiramente vamos construir o gráfico para uma melhor visualização.

Cálculo do volume dos sólidos de revolução

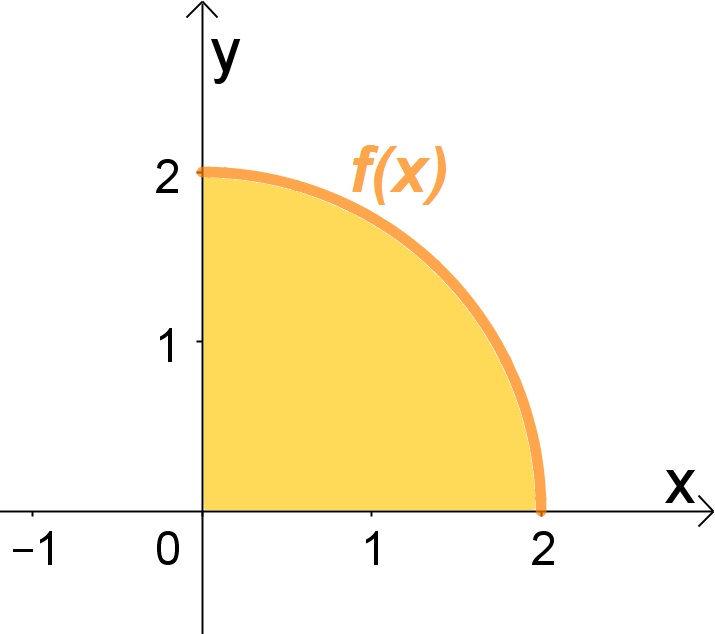
Observe que f(x) é a parte positiva de uma circunferência e com o domínio indicado temos apenas um quarto de circunferência. Assim, calcularemos o volume pela integral e, em seguida, aplicaremos a fórmula do volume de esfera para percebermos a igualdade.

Aplicando a fórmula do volume dos sólidos de revolução, temos

$\displaystyle V=\int_{0}^{2}\pi\big(\sqrt{4-x^{2}}\big)^{2}dx=\pi \int_{0}^{2}4-x^{2}dx$ .

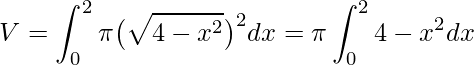Dessa forma, aplicando as propriedades das integrais temos

$\displaystyle V=\pi \int_{0}^{2}4-x^{2}dx=\pi\bigg(4x-\frac{x^{3}}{3}\bigg)\bigg|_{0}^{2}=\frac{16\pi}{3}$ .

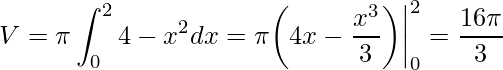Agora aplicando a fórmula do volume de esfera

$\displaystyle V_{esfera}=\frac{4\pi r^{3}}{3}$ .

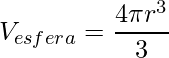Lembrando que devemos dividir por 2, pois temos apenas meia esfera. Assim, aplicando temos

$\displaystyle V_{esfera}=\frac{4\pi 2^{3}}{3\cdot 2}=\frac{16\pi}{3}$

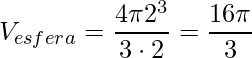
que é a igualdade que buscávamos.

2) $\displaystyle f(x)=3-x^{2}$ e $\displaystyle g(x)=-\sqrt{3}x+3$ entorno do eixo y entre os pontos de intersecção.

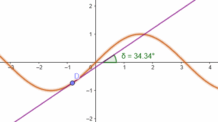
Primeiramente vamos construir o gráfico para uma melhor visualização.

Cálculo do volume dos sólidos de revolução II

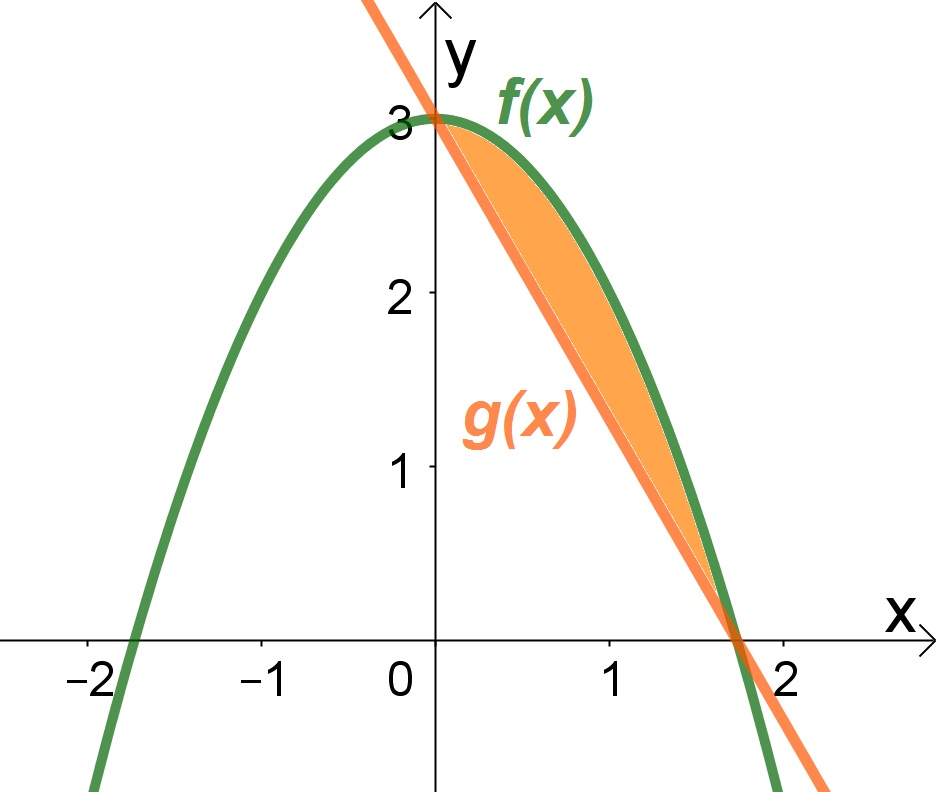
Observe que temos as funções dependendo de x, mas como giramos entorno do eixo y, temos que reescreve-la em função de y. Mas primeiro vamos encontrar os pontos de intersecção ao igualarmos as duas funções.

$\displaystyle f(x)=g(x)$

$\displaystyle 3-x^{2}=-\sqrt{3}x+3\:\Rightarrow\: x^{2}-\sqrt{3}x=0\:\Rightarrow\: x(x-\sqrt{3})=0$

Assim para termos a última igualdade x deve ser $\displaystyle x=0$ ou $\displaystyle x=\sqrt{3}$ , logo os pontos são $\displaystyle (0,3)$ e $\displaystyle (\sqrt{3},0)$ .

Agora, transformando as funções, devemos insolar a variável x

$\displaystyle y=3-x^{2}\:\Rightarrow\: x^{2}=3-y\:\Rightarrow\: x=\sqrt{3-y}$

$\displaystyle y=-\sqrt{3}x+3\:\Rightarrow\: \sqrt{3}x=3-y\:\Rightarrow\: x=\frac{3-y}{\sqrt{3}}$ .

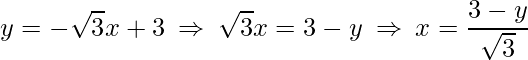Assim temos $\displaystyle f(y)=\sqrt{3-y}$ e $\displaystyle g(y)=\frac{3-y}{\sqrt{3}}$ .

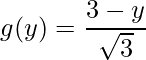Finalmente, temos todas as informações para aplicarmos as integrais. Entretanto, só mais uma observação, note que f(y) é maior do que g(y) no interior do intervalo de integração. Portanto, devemos subtrair o volume gerado por g(y) daquele gerado por f(y). Assim

$\displaystyle V=\pi\int_{a}^{b} \big(f(y)\big)^{2}dy-\pi\int_{a}^{b} \big(g(y)\big)^{2}dy=\pi\int_{a}^{b} \big(f(y)\big)^{2}-\big(g(y)\big)^{2}dy$ .

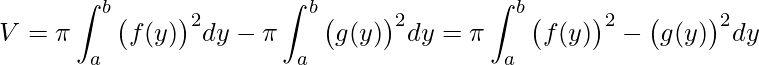Aplicando temos

$\displaystyle V=\pi\int_{0}^{3} \big(\sqrt{3-y}\big)^{2}-\bigg(\frac{3-y}{\sqrt{3}}\bigg)^{2}dy=$

$\displaystyle \pi\int_{0}^{3}3-y-\bigg(\frac{9-6y+y^{2}}{3}\bigg)dy=\pi\int_{0}^{3}\frac{3y-y^{2}}{3}dy=$

$\displaystyle \frac{\pi}{3}\bigg(\frac{3y^{2}}{2}-\frac{y^{3}}{3}\bigg)\bigg|_{0}^{3}=\frac{\pi}{3}\bigg(\frac{27}{2}-\frac{27}{3}\bigg)=\pi\bigg(\frac{9}{2}-3\bigg)=1,5\pi$ .

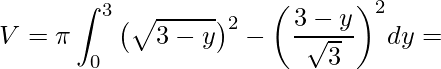
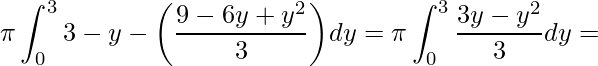
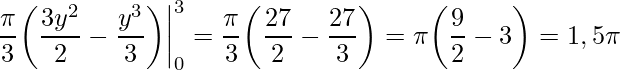Este último exercício, resolvemos aqui também usando a fórmula específica para revolução entorno do eixo y. Assim obtemos o resultado desejado, caso você ficou em dúvida em algum passo, nos deixe seu comentário.

Cálculo do volume dos sólidos de revolução

Baixe de forma gratuita nossos Ebooks e treinamentos

Cálculo do volume dos sólidos de revolução – exercícios resolvidos

Determine o volume do objeto gerado ao girarmos a\as função\funções entorno do eixo dado no domínio indicado.

Compartilhe agora mesmo:

Indeterminação no cálculo dos Limites

Funções exponenciais e suas características

Exemplo 4 – Domínio e Imagem de uma Função Racional

Para enviar seu comentário, preencha os campos abaixo:

Deixe um comentário Cancelar resposta

Seja o primeiro a comentar!

Damos valor à sua privacidade

Cookies estritamente necessários

Cookies de desempenho

Cookies de funcionalidade

Cookies de publicidade

Baixe de forma gratuita nossos Ebooks e treinamentos

Cálculo do volume dos sólidos de revolução – exercícios resolvidos

Determine o volume do objeto gerado ao girarmos a\as função\funções entorno do eixo dado no domínio indicado.

Compartilhe agora mesmo:

Indeterminação no cálculo dos Limites

Funções exponenciais e suas características

Exemplo 4 – Domínio e Imagem de uma Função Racional

Para enviar seu comentário, preencha os campos abaixo:

Deixe um comentário Cancelar resposta

Seja o primeiro a comentar!

Damos valor à sua privacidade

Cookies estritamente necessários

Cookies de desempenho

Cookies de funcionalidade

Cookies de publicidade

Faça aulas personalizadas sobre conteúdos específicos de Matemática e Raciocínio Lógico