Calculando a área da superfície de um sólido de revolução

Neste post apresentaremos um novo exemplo do Cálculo da área da superfície de um sólido de revolução. Lembrando que já publicamos de forma resumida a construção da fórmula que calcula a área das superfícies, também chamada de casca de um objeto. Assim, nos dedicaremos hoje para mais um exemplo, porém hoje entorno do eixo y.

Primeiramente recorde que a fórmula é dada por

$\displaystyle S=2\pi \int_{a}^{b}f(y)\sqrt{1+\Big({f}'(y)\Big)^{2}}dy$

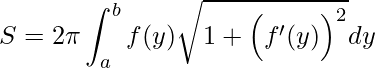
ao girarmos f(y) entorno do eixo y.

Determine a área da casca do objeto gerado ao girarmos a função f(y) entorno do eixo y onde

$\displaystyle f(y)=e^{y}$ e $\displaystyle y\in[0,1]$ .

O primeiro passo para encontrarmos a solução é derivar a função dada.

$\displaystyle{f}'(y)=e^{y}$

Agora que devemos substituir os elementos na fórmula

$\displaystyle S=2\pi\int_{0}^{1} e^{y}\sqrt{1+e^{2y}}dy$ .

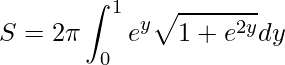Para resolvermos esta integral, aplicaremos o método de integração por substituição. Onde tomemos

$\displaystyle u=e^{y}$

e derivando

$\displaystyle du=e^{y}dy$ .

Lembre-se que também devemos converter o intervalo de integração. Assim temos

$\displaystyle S=2\pi \int_{1}^{e}\sqrt{1+u^{2}}du$ .

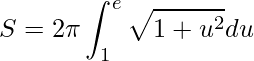Observe que agora chegamos em uma integral que para ser resolvida devemos aplicar Substituição Trigonométrica. Como já resolvemos uma questão semelhante a esta (aqui), pularemos algumas partes.

Após fazer as relações trigonométricas e substituindo cada expressão na integral original teremos

$\displaystyle S=2\pi \int sec^{3}(\theta)d\theta$ .

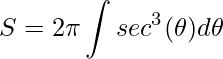(Para não converter novamente o intervalo de integração, deixamos para aplicar quando retornarmos a variável u). A integral de potências da função secante são encontradas em formulários presentes em muitos livros. Ou se quiser acompanhar passo a passo, volte ao link que acabamos de indicar (nele usamos interação por partes). Resolvendo esta integral teremos

$\displaystyle S=\pi (u\sqrt{1+u^{2}}+\ln|\sqrt{1+u^{2}}+u|)\big|^{e}_{1}$ .

Aplicando os limites de integração obtemos

$\displaystyle S=\pi (e\sqrt{1+e^{2}}+\ln|\sqrt{1+e^{2}}+e|-\sqrt{2}-\ln|\sqrt{2}+1|)$ .

Na figura a seguir temos a representação da revolução da função dada.

área da superfície de um sólido de revolução

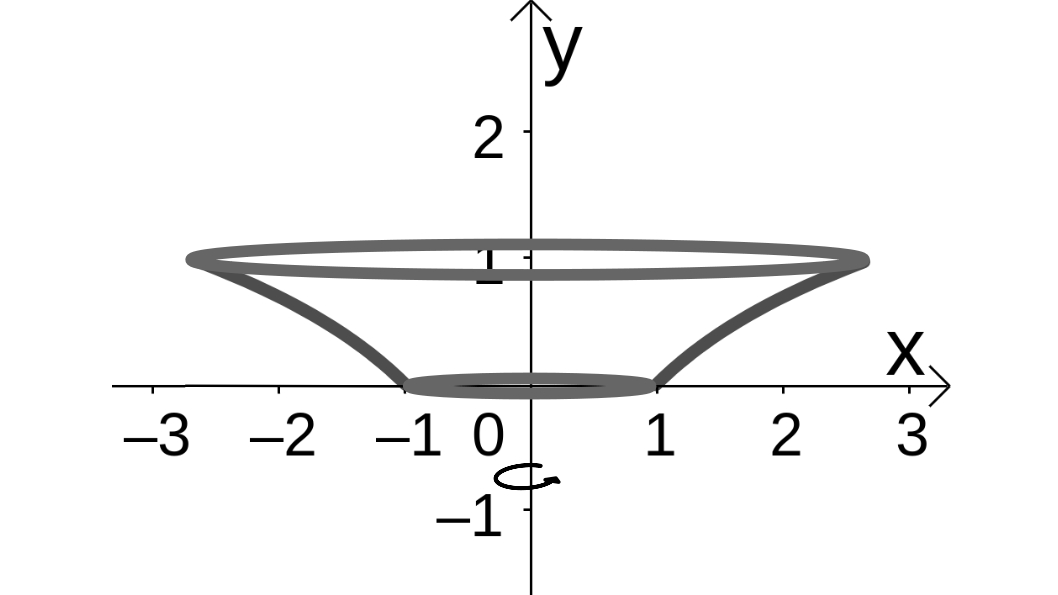
Caso surgiu alguma dúvida, deixe ela nos comentários a seguir que buscaremos esclarecer.

Calculando a área da superfície de um sólido de revolução

Baixe de forma gratuita nossos Ebooks e treinamentos

Calculando a área da superfície de um sólido de revolução

Determine a área da casca do objeto gerado ao girarmos a função f(y) entorno do eixo y onde

Compartilhe agora mesmo:

Relações Trigonométricas

Taxas relacionadas explicação e exemplo resolvido

Problemas resolvidos de máximos e mínimos – Exercício resolvido

Para enviar seu comentário, preencha os campos abaixo:

Deixe um comentário Cancelar resposta

Seja o primeiro a comentar!

Damos valor à sua privacidade

Cookies estritamente necessários

Cookies de desempenho

Cookies de funcionalidade

Cookies de publicidade

Baixe de forma gratuita nossos Ebooks e treinamentos

Calculando a área da superfície de um sólido de revolução

Determine a área da casca do objeto gerado ao girarmos a função f(y) entorno do eixo y onde

Compartilhe agora mesmo:

Relações Trigonométricas

Taxas relacionadas explicação e exemplo resolvido

Problemas resolvidos de máximos e mínimos – Exercício resolvido

Para enviar seu comentário, preencha os campos abaixo:

Deixe um comentário Cancelar resposta

Seja o primeiro a comentar!

Damos valor à sua privacidade

Cookies estritamente necessários

Cookies de desempenho

Cookies de funcionalidade

Cookies de publicidade

Faça aulas personalizadas sobre conteúdos específicos de Matemática e Raciocínio Lógico