Resolvendo Integral usando duas técnicas: Integração por partes e Integração por substituição
Neste post estaremos Resolvendo Integral usando duas técnicas: Integração por partes e Integração por substituição. Caso queira rever estas duas técnicas com mais detalhes clique nos links a seguir: Integração por partes e Integração por substituição.
Resolva: 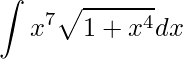
O primeiro passo para utilizarmos a Integração por partes é definirmos as funções u(x) e dv. Entretanto, para resolver esta integral temos um truque, que é abrir o termo da potência sétima em duas
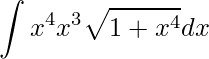 .
.
Assim, tomando
e
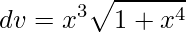 .
.
Aqui observe que temos que integrar esta segunda equação, onde aplicamos a Técnica da Integração por substituição. Assim, tomando ![]() e derivando
e derivando 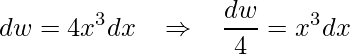 , substituindo
, substituindo
Aplicando a técnica da Integração por partes temos
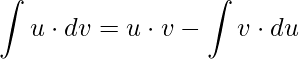 .
.
Substituindo,
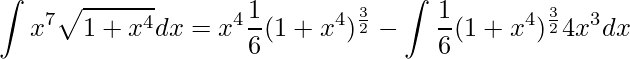
Perceba que após aplicarmos a Integração por Partes, temos uma nova integral, em que podemos utilizar novamente a Integração por substituição. Onde chamamos ![]() e derivando
e derivando ![]() . Assim, substituindo na integral temos
. Assim, substituindo na integral temos
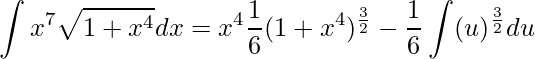 .
.
Por fim, resolvendo esta última integral obtemos o resultado desejado
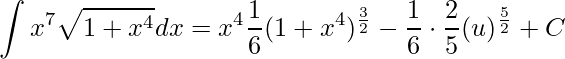 ,
,
substituindo e simplificando
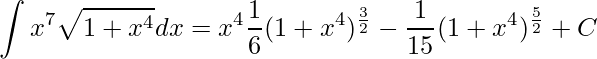 .
.

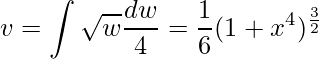

Deixe um comentário