Volumes dos sólidos de revolução entorno do eixo y
A base do cálculo dos Volumes dos sólidos de revolução entorno do eixo y é semelhante ao caso entorno de x, onde devemos fatiar o domínio. Entretanto, neste devemos saber calcular o volume de cada uma destas fatias (camadas cilíndricas). Em seguida, formar uma soma de Riemann e fazer a espessura destas camadas tender a zero (limite).
Determinando a fórmula do Volumes dos sólidos de revolução entorno do eixo y
Primeiramente apresentamos uma imagem ilustratíva da formação do sólido.
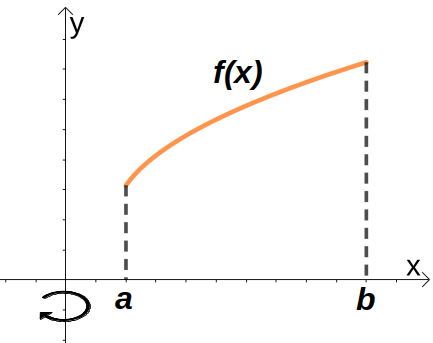
Por tanto, o sólido é formado ao girarmos o objeto delimitado pela função f(x) e as retas x=a, x=b e y=0 entormo do eixo y. Em seguida, fatiamos o sólido em N camadas cilíndricas (anéis), onde cada anel é definido do raio ri até ri+1, como vemos na figura.
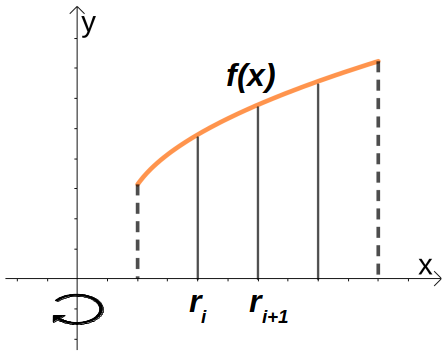
Desta forma, o volume do anel Vi+1 é dado por
![]() ,
,
onde hi+1 é a altura do anel Vi+1 e observe que a equação anterior é a expressão da subtração do volume de dois cilíndros. Manipulando a equação dada utilizando produtos notáveis temos
![]()
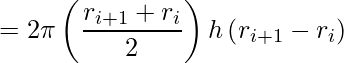 .
.
Observe que o termo do primeiro parenteses é o ponto médio do anel, ou seja, 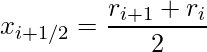 , e no segundo parenteses é a expessura do anel Vi+1
, e no segundo parenteses é a expessura do anel Vi+1 ![]() . Volume deste anel pode ser escrito como
. Volume deste anel pode ser escrito como
![]() .
.
Em seguida, somando todos os volumes dos anéis teremos um volume aproximado do sólido de revolução
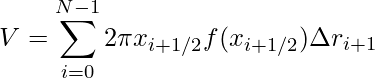 .
.
Por fim, tomando o limite de N tendendo ao infinito teremos ![]() e
e
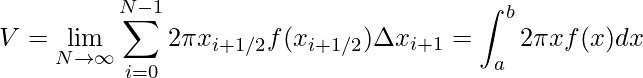 .
.
Definição
Seja uma função f(x) continua não negativa em [a,b], então o volume de revolução V formado ao girarmos a função f(x) definida entre [a,b] entorno do eixo y e limitado por y=0 é determinado por
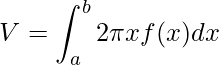 .
.



Deixe um comentário