Volumes de revolução entorno do eixo y – exercícios resolvidos
Neste post resolveremos alguns Volumes de revolução entorno do eixo y. Aplicaremos a fórmula apresentado no post anterior em alguns exercícios. Se você quiser acompanhar a resolução de exercícios entorno do eixo x clique aqui.
Primeiramente, reapresentamos a definição da fórmula que iremos utilizar.
Definição
Seja uma função f(x) continua não negativa em [a,b], então o volume de revolução V formado ao girarmos a função f(x) definida entre [a,b] entorno do eixo y e limitado por y=0 é determinado por
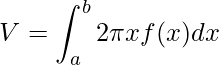 .
.
Determine o volume do objeto gerado ao girarmos as funções f(x) e g(x) entorno do eixo y entre os pontos de intersecção.
![]() e
e ![]()
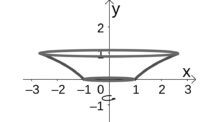
Para uma melhor compreensão do problema, geramos o gráfico das duas funções.
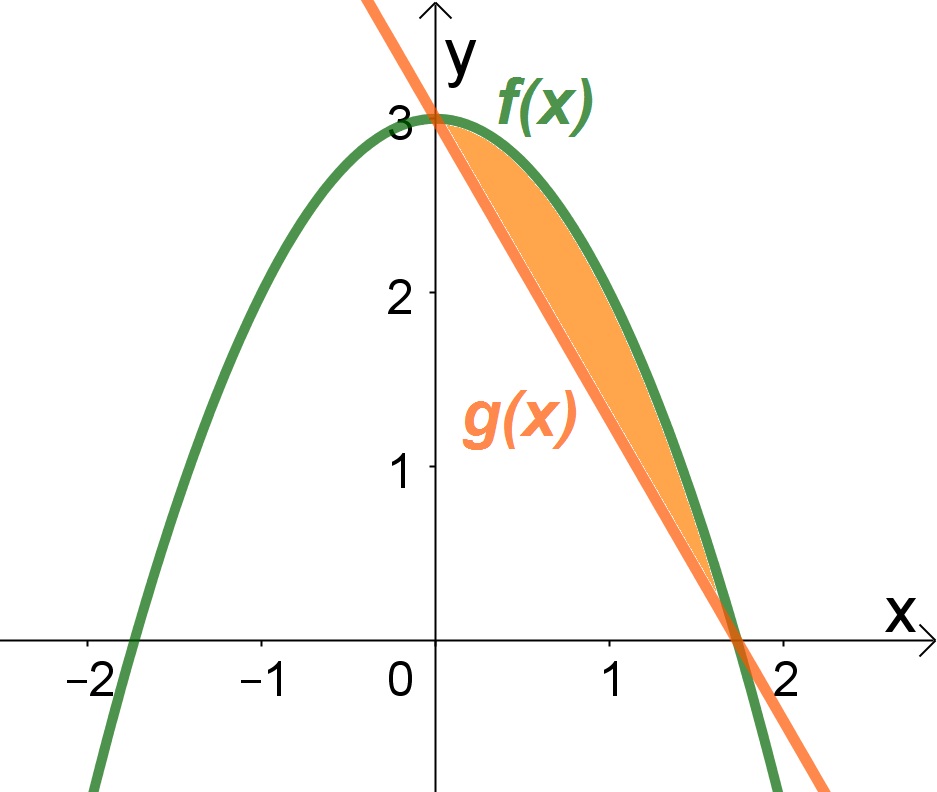
Mas primeiro vamos encontrar os pontos de intersecção ao igualarmos as duas funções.
![]()
![]()
Assim para termos a última igualdade x deve ser ![]() ou
ou ![]() , logo os pontos são
, logo os pontos são ![]() e
e ![]() .
.
Agora, aplicamos a definição, mas antes observe que a função f(x) é maior do que g(x) no intervalo de integração. Assim, temos
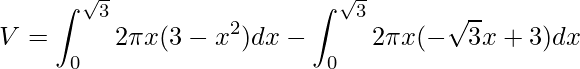 .
.
Como temos o mesmo intervalo de integração, podemos reescrever como uma única integral. Além disto, aproveitamos para associarmos os termos em comum
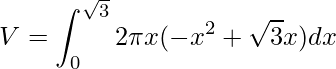
e retirar o ![]() do integrando, uma vez que, ele não depende de x, assim temos
do integrando, uma vez que, ele não depende de x, assim temos
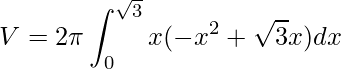 .
.
No integrando temos uma multiplicação de polinômios, que resultará também em um polinômio. Assim, nosso problema se resume em integrar um polinômio. Portanto, temos
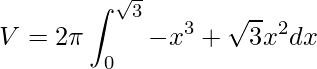 .
.
No integrando esta última equação teremos
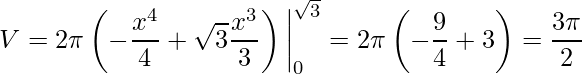 .
.
Observe que no exercício 2 do post passado já tinhamos resolvido este exercício. Porém, lá utilizamos a fórmula para os casos de revolução entorno do eixo x. Ambos podem ser utilizadas, você pode escolher a que melhor lhe convém.




Deixe um comentário