Problema de Máximos e Mínimos – Exercícios resolvidos

No post de hoje resolveremos mais um Problema de máximos e mínimos. Neste tipo problema necessitamos encontrar os pontos onde a função dada assume seu maior valor (máximo) ou menor valor (mínimo) em um determinado intervalo. Há um tempo atrás já publicamos um post explicando um pouco sobre os pontos de máximo e de mínimo local. Caso queira rever clique aqui.

Resolva o problema de máximos e mínimos a seguir:

Uma área de terra retangular está limitada por um arame em três de seus lados e por um rio reto no quarto lado. Ache as dimensões da terra com área máxima que pode ser cercada com 1.000 metros de arame.

Este é um problema simples de máximos e mínimos, porém resolveremos com calma para você compreender todos os detalhes. Uma dica importante para o entendimento deste tipo de exercício é desenhar um esboço, para que possamos visualizar o problema. O problema diz que é uma área de terra retangular, portanto, os lados opostos possuem mesmo comprimento.

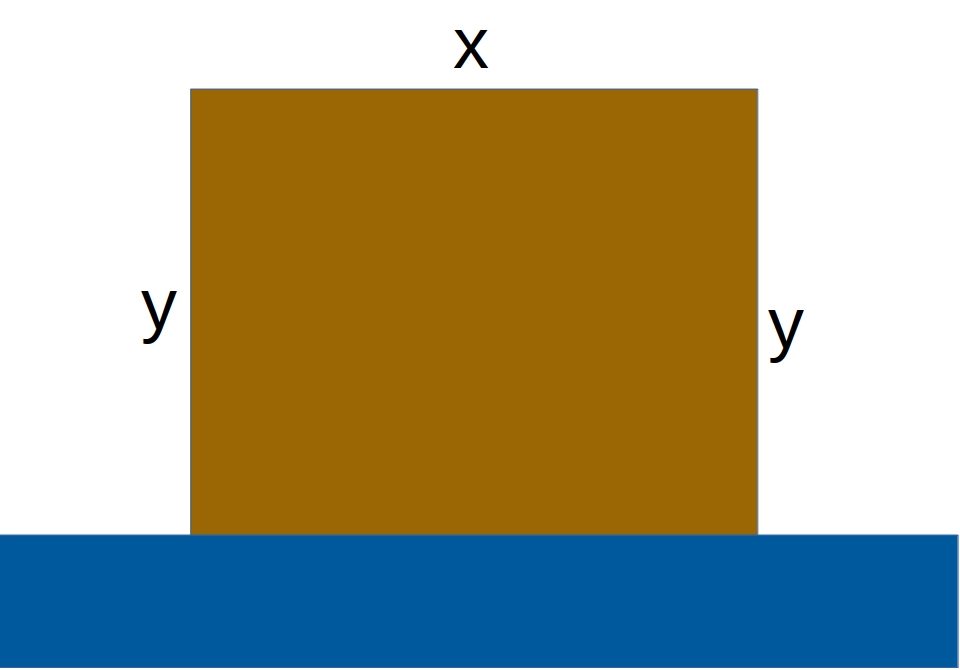
O problema nos fala que temos 1000m de arame para cercar o terreno e que um dos lados não precisamos cercar. Assim, sobram o lado oposto ao rio (lado x) e os outros dois lados que são paralelos entre si (lados y). Portanto, somando os três lados temos

.

O problema nos pede as dimensões da terra para termos área máxima. Desta maneira, vamos relembrar a fórmula da área de um retângulo

.

Assim, tomando a equação anterior e isolando x teremos

,

que substituindo na fórmula da área do retângulo teremos

.

Observe que a área é uma função que depende do comprimento y, então, temos que

.

Os próximos passos para encontrar os pontos de máxima área é derivar a função A(y) e igualarmos a zero. Observe que temos uma função polinomial, em que é formada por soma de potências, logo temos derivadas de potência. Derivando teremos

e igualando a zero e isolando a variável y teremos

.

Dessa forma, encontramos o comprimento de um dos lados, para encontrar o outro basta substituir na equação que somando os três lados temos

onde encontramos o lado que nos faltava

.