Integração de funções racionais por frações parciais – Exercício resolvido
No post de hoje resolveremos um exemplo de integral utilizando Integração de funções racionais por frações parciais. A ideia principal deste método é fatorar a função racional mais “complicada” em funções mais “fáceis”. Acompanhe a resolução, qualquer dúvida deixe seu comentário.
Faça a integração da seguinte função racional:
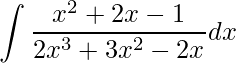 .
.
O primeiro passo para aplicarmos o método de Integração de funções racionais através das frações parciais é fatorar o denominador. Se conseguirmos obter fatores lineares (1º grau) torna a integração mais fácil. Entretanto, se não for possível podemos fatorar em graus maiores, porém quanto maior o grau torna a integração mais trabalhosa.
Observe que todos os termos da função do denominador possuem a variável x, isto indica que uma das raizes é o zero. Assim, fatorando temos
![]() .
.
Para fatoral a função de segundo grau que está dentro do parenteses podemos aplicar fórmula de Bhaskara. Dessa forma, encontraremos as outras duas raízes: ![]() e
e ![]() . Entretanto, tenha o cuidado, pois infinitos polinômios possuem o mesmo conjunto de raízes. Observe que se multiplicarmos os três fatores lineares teremos
. Entretanto, tenha o cuidado, pois infinitos polinômios possuem o mesmo conjunto de raízes. Observe que se multiplicarmos os três fatores lineares teremos
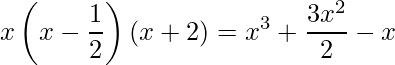
que é diferente do denominador da nossa integral. Portanto, temos que ajustar, observe que o coeficiente do termo de maior grau do denominador da integral é 2. Este é um indicativo que devemos multiplicar a nossa fatoração por 2. Como temos três fatores, por conveniência, nós multiplicaremos o segundo fator, assim temos
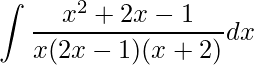 .
.
Se você fizer as multiplicações obterá a integral original. O próximo passo para decompormos a função racional é determinar os coeficientes para cada fator linear
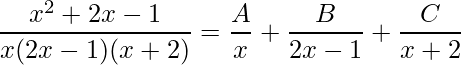 .
.
Se multiplicarmos ambos os lados da expressão anterior por ![]() obteremos
obteremos
![]() .
.
Para determinar os coeficientes A, B e C existem várias formas, nós indicamos a que julgamos mais rápida e fácil. O técnica consiste em substituir na variável x os valores das raízes. Ou seja, se substituimos x=0 temos
![]()
logo 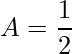 . Se substituimos x=1/2 temos
. Se substituimos x=1/2 temos
![]()
![]()
logo 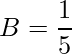 . Se substituimos x=-2 temos
. Se substituimos x=-2 temos
![]()
![]()
logo 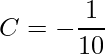 .
.
Desta forma obtemos as frações parciais que facilitam a integração. Assim, temos
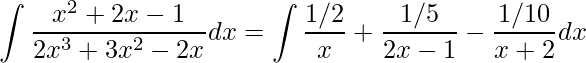
que pode ser reescrita como
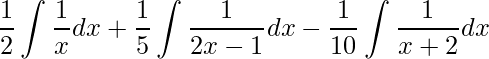 .
.
As novas integrais são todas resolvidas utilizando a integração direta 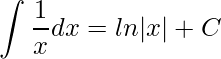 . Entretanto, a segunda e terceira integral temos que fazer primeiro uma substituição, onde obteremos a seguinte solução
. Entretanto, a segunda e terceira integral temos que fazer primeiro uma substituição, onde obteremos a seguinte solução
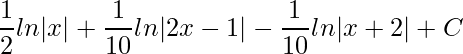 .
.



Deixe um comentário