Alguns exercícios resolvidos de logaritmos
Neste post apresentaremos alguns exercícios resolvidos de logaritmos. Para isso, devemos utilizar as Propriedades dos Logaritmos que postamos anteriormente.
Exercícios resolvidos de logaritmos passo a passo
1) (UFRGS – 2018) Se 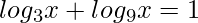 , então qual é o valor de x.
, então qual é o valor de x.
Primeiramente, observe que temos uma equação com dois logaritmos de bases diferentes. Assim precisamos manipular os logaritmos a fim de obter uma equação com uma única base. Podemos escolher como base 3, 9 ou ainda uma outra base. Entretanto, aconselho escolher como base 3 ou 9, assim precisamos manipular apenas um dos logaritmos. Se escolhermos 3 ou 9 obteremos o mesmo resultado, como veremos a seguir.
1ª proposta: mudança de base para a base 9
Utilizando a propriedade de mudança de base para ![]() temos
temos
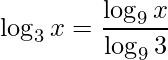 .
.
Onde
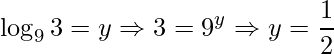 .
.
Assim temos
![]()
e substituindo na equação original temos
![]()
![Rendered by QuickLaTeX.com \displaystyle 3\log_{9}x=1\Rightarrow \log_{9}x=\frac{1}{3}\Rightarrow x=9^{\frac{1}{3}}\Rightarrow x=\sqrt[3]{9}](https://dicasdecalculo.net/wp-content/ql-cache/quicklatex.com-9d013e7ab40b322a34c8d3669d710e5b_l3.png) .
.
2ª proposta: mudança de base para a base 3
Utilizando a propriedade de mudança de base para ![]() temos
temos
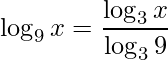 .
.
Onde
![]() .
.
Assim temos
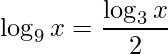
e substituindo na equação original temos
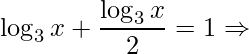
![Rendered by QuickLaTeX.com \displaystyle \frac{3\log_{3}x}{2}=1\Rightarrow \log_{3}x=\frac{2}{3}\Rightarrow x=3^{\frac{2}{3}}\Rightarrow x=\sqrt[3]{9}](https://dicasdecalculo.net/wp-content/ql-cache/quicklatex.com-26120c1a7413293b0c1fa826371b68b4_l3.png) .
.
Dessa forma, obtemos o resultado por duas maneiras diferentes.
2) (UDESC-2008) Se 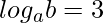 e
e 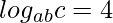 , então qual é o valor de
, então qual é o valor de 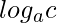 .
.
Neste tipo de exercício devemos manipular o logaritmo que queremos solucionar a fim de usar as informações dadas pelo problema. Para isto, iniciamos fazendo uma mudança de base “ao contrário”
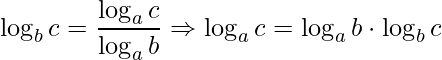 .
.
O primeiro logaritmo do lado direito é fornecido pelo problema, na qual precisamos apenas substituir o valor dado. Desta forma, temos o seguinte problema
![]() .
.
Para resolver este segundo logaritmo utilizaremos a outra informação dada pelo problema. Para isto precisamos fazer uma nova mudança de base
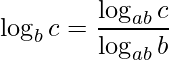 .
.
Que substituindo a informação dada pelo problema temos
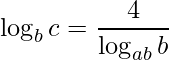
e ao substituir esta parte no problema que estamos resolvendo temos
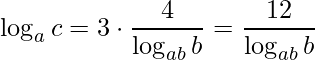 .
.
Por fim, precisamos de mais uma mudança de base
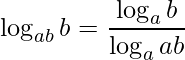
e aplicando a Propriedade do Produto dos logaritmos no denominador temos
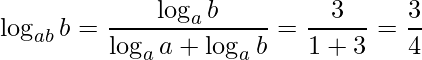 .
.
Para finalizar, precisamos apenas substituir e fazer a operação da divisão de frações
 .
.



Deixe um comentário