Alguns exercícios resolvidos de logaritmos – Parte 2
Neste post continuaremos a apresentar alguns exercícios resolvidos de logaritmos. Para isso, utilizaremos as Propriedades dos Logaritmos que postamos anteriormente.
Exercícios resolvidos de logaritmos passo a passo
1) (FUVEST – 2019) Se 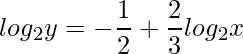 , para x>0, então
, para x>0, então
a)
b)
c)
d)
e)
Primeiramente, observe que temos na equação dois logaritmos de bases iguais. Assim, podemos “uní-los” utilizando a Propriedade do Quociente dos Logaritmos. Dessa forma, primeiro isolamos os logaritmos no lado esquerdo da equação e aplicamos a propriedade da potência.
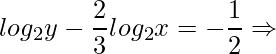
![Rendered by QuickLaTeX.com \displaystyle log_{2} y-log_{2}x^{\frac{2}{3}}=-\frac{1}{2}\Rightarrow log_{2} y-log_{2}\sqrt[3]{x^{2}}=-\frac{1}{2}](https://dicasdecalculo.net/wp-content/ql-cache/quicklatex.com-da33e4b059a62853096c85c018113e3a_l3.png)
Em seguida, aplicamos a propriedade do quociente, na qual obtemos
![Rendered by QuickLaTeX.com \displaystyle log_{2} \frac{y}{\sqrt[3]{x^{2}}}=-\frac{1}{2}](https://dicasdecalculo.net/wp-content/ql-cache/quicklatex.com-1abbbea1f27ca4f55c653c5a574ca1d1_l3.png) .
.
Por fim, aplicamos a operação do logaritmo
![Rendered by QuickLaTeX.com \displaystyle \frac{y}{\sqrt[3]{x^{2}}}=2^{-\frac{1}{2}}\Rightarrow](https://dicasdecalculo.net/wp-content/ql-cache/quicklatex.com-5d6dd23bec1644d26ce8c3237c0ebd63_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \frac{y}{\sqrt[3]{x^{2}}}=\frac{1}{\sqrt{2}}\Rightarrow y=\frac{\sqrt[3]{x^{2}}}{\sqrt{2}}](https://dicasdecalculo.net/wp-content/ql-cache/quicklatex.com-86ce510cac30ce3fbe782ffa6cd14aad_l3.png) .
.
Portanto, a resposta é a letra a.
2) (UFMG 2009) Numa calculadora científica, ao se digitar um número positivo qualquer e, em seguida, se apertar a tecla log, aparece, no visor, o logaritmo decimal do número inicialmente digitado. Digita-se o número 10.000 nessa calculadora e, logo após, aperta-se, N vezes, a tecla log, até aparecer um número negativo no visor. Então, é CORRETO afirmar que o número N é igual
a) 2
b) 3
c) 4
d) 5
Primeiramente, observe que o enunciado fala que a tecla log é o logaritmo decimal, ou seja, de base 10. Assim, cada vez que apertamos a tecla estamos obtemos o logaritmo de base 10 do resultado anterior. Desta forma, iniciamos digitando o número 10.000
Clicar 1ª vez a tecla log
Ao clicar a tecla log, a calculadora irá fazer
![]() ,
,
onde no visor aparecerá o resultado da seguinte conta
![]() .
.
Logo,
![]() .
.
Portanto, no visor da calculadora irá aparecer o número 4. Assim, com N=1 ainda temos valor positivo.
Clicar 2ª vez a tecla log
Ao clicar pela segunda vez a tecla log, a calculadora irá fazer
![]() .
.
Aqui vale lembrar que esta é uma questão de vestibular e, portanto, não temos uma calculadora em mãos. O objetivo desta questão é obter a solução apenas utilizando as propriedades dos logaritmos.
Observe que nenhuma potência inteira de 4 é igual a 10, Dessa forma, ![]() será um número decimal. Para termos uma aproximação desse resultado utilizaremos a propriedade de mudança de base
será um número decimal. Para termos uma aproximação desse resultado utilizaremos a propriedade de mudança de base
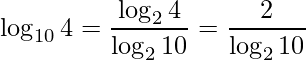 .
.
Nesta última igualdade apenas aplicamos o operador logaritmo no numerador, como, 4 é 2 na potência 2, obtemos 2 no numerador. Para o denominador utilizaremos a seguinte análise se 8<10<16 então
![]() .
.
Como ![]() e
e ![]() temos que
temos que
![]() .
.
Lembre que tinhamos 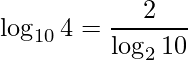 . Portanto,
. Portanto,
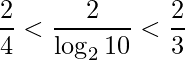 .
.
OBS: quanto maior for o denominador de um mesmo número, menor será o valor da fração.
Portanto, com N=2 ainda temos valor positivo.
Clicar 3ª vez a tecla log
Como não temos um valor exato da segunda vez que clicamos na tecla log, analizaremos os dois extermos da desigualdade anterior.
Iniciamos aplicando a propriedade do quociente dos logaritmos
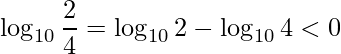 ,
,
pois ![]() e ambas logaritmos tem mesma base. Portanto, sabemos que o lado esquerdo da desiqualdade é negativo. Caso o lado direito também será negativo obtemos o resultado da questão.
e ambas logaritmos tem mesma base. Portanto, sabemos que o lado esquerdo da desiqualdade é negativo. Caso o lado direito também será negativo obtemos o resultado da questão.
Iniciamos novamente aplicando a propriedade do quociente dos logaritmos
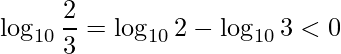 ,
,
pois ![]() e ambas logaritmos tem mesma base. Portanto, como ambos lados de
e ambas logaritmos tem mesma base. Portanto, como ambos lados de
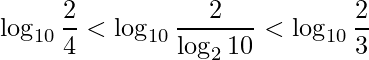
são valores negativos temos que
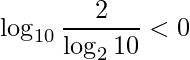 .
.
Portanto, a resposta é a letra b.

![Rendered by QuickLaTeX.com \displaystyle y=\frac{\sqrt[3]{x^{2}}}{\sqrt{2}}](https://dicasdecalculo.net/wp-content/ql-cache/quicklatex.com-d07be994b4ce68a526e99cf3728bcee2_l3.png)
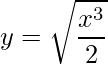
![Rendered by QuickLaTeX.com \displaystyle y=-\frac{1}{\sqrt{2}}+\sqrt[3]{x^{2}}](https://dicasdecalculo.net/wp-content/ql-cache/quicklatex.com-31dcb5e4781482d765be0b690dac7d69_l3.png)
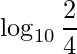
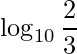


Deixe um comentário