Problemas que envolvem o conteúdo de funções
Os Problemas que envolvem o conteúdo de funções são aqueles em que precisamos interpretar um pequeno texto e retirar dele os dados do problema para em seguida resolvermos. Em geral, os problemas apresentam um problema real, entretanto, bem simplificado. No post de hoje apresentaremos apenas um problema, mas posteriormente apresentaremos outros mais.
Problema resolvido de funções passo a passo
(UA – AM) Após várias experiências em laboratório, observou-se que a concentração de certo antibiótico, no sangue de cobaias, varia de acordo com a função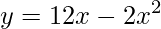 
, em que x é o tempo decorrido, em horas, após a ingestão do antibiótico. Nessas condições, determine o tempo necessário para que o antibiótico atinja nível máximo de concentração no sangue dessas cobaias.
Primeiramente, note que a função dada é uma função de segundo grau (ordem). Este tipo de função já apresentamos anteriormente, na qual apenas observando a função podemos retirar algumas informações. Dessa forma, observe que o exercício pede para determinar o ponto onde a função alcança seu maior valor (ponto de máximo). Como a função dada é uma função do segundo grau e o coeficiente a (aquele que acompanha o termo de segunda ordem) é negativo, temos uma parábola voltada para baixo. Portanto, temos um único ponto em que a função atinge seu máximo e ele é chamado de vértice da função.
Desta forma, o que devemos fazer é determina o valor do vértice na variável y, ou seja, 
. Para determinar o vértice y, você pode utilizar a fórmula em que já apresentamos aqui,
,
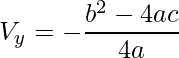onde a=-2, b=12 e c=0 (as letras correspondem a 
). Portanto temos,
.
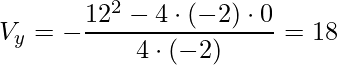Entretanto, caso você não lembre da fórmula, você pode determinar as raízes (
). Em seguida, calcular o ponto médio entre as raízes, (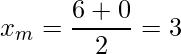
) e aplicar o ponto médio na função dada (
). Assim, obtemos o mesmo valor sem precisar da fórmula. A seguir, apresentamos o gráfico desta função juntamente com os pontos citados neste texto.
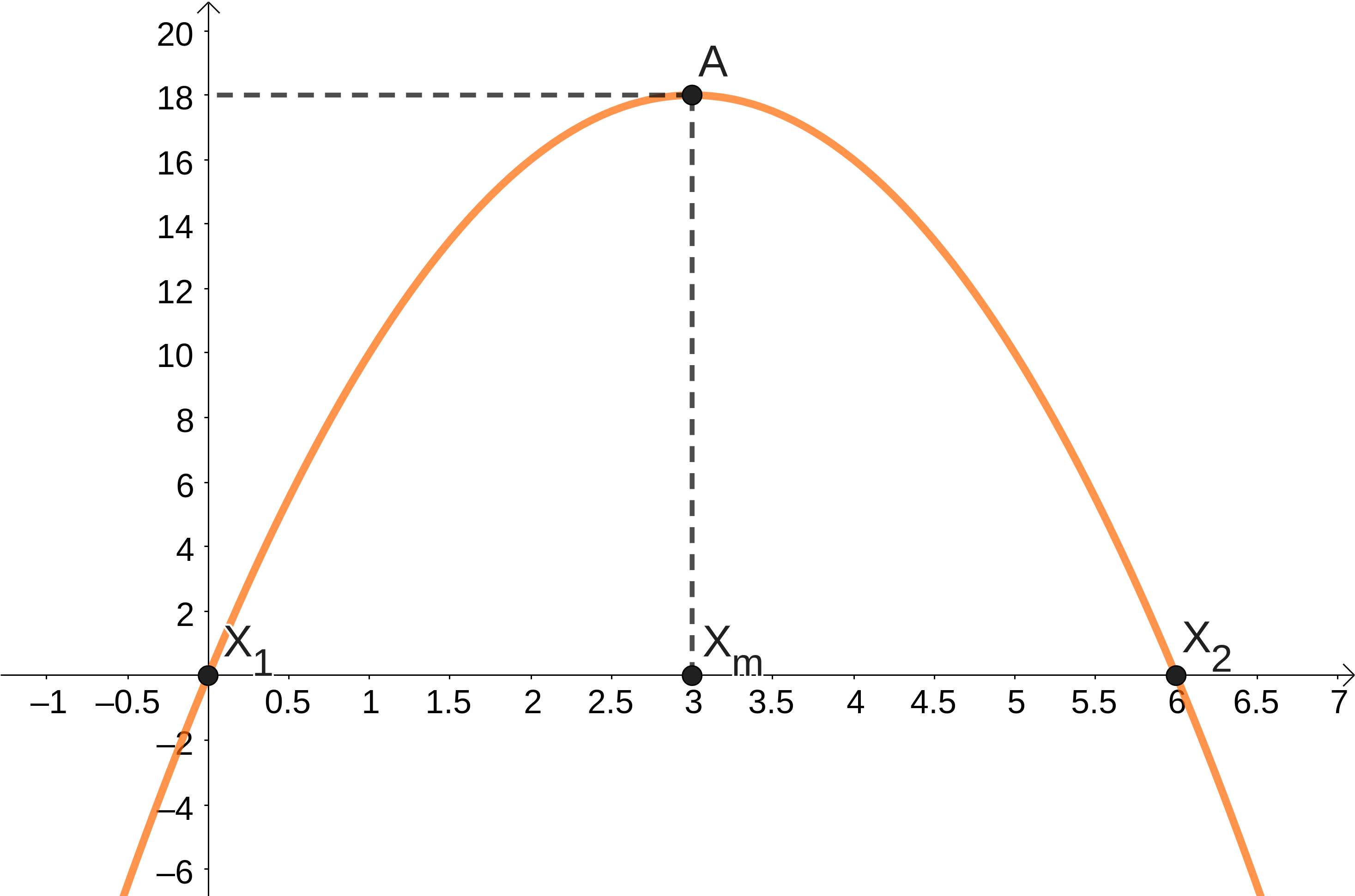
Portanto, a concentração máxima de antibiótico no sangue das cobaias ocorre 3 horas após a ingestão e com uma concentração igual a 18.
