Teoria dos conjuntos: exercício resolvido
Neste post resolveremos um exercício sobre a Teoria dos conjuntos. A Teoria dos conjuntos é outro conteúdo bastante cobrado em concursos públicos. Este conteúdo estuda a relação entre conjuntos, que são coleções de elementos.
(INSS 2016 Técnico) Julgue o item a seguir se verdadeiro ou falso.
( ) Se A, B e C forem conjuntos quaisquer tais que A,B⊂ C, então (C\A) ∩ (A ∪ B)=C ∩ B.
Resolução:
Primeiramente, note que o exercício apenas diz que A e B estão contidos em C, A,B⊂ C. Porém, não nos diz qual é a relação entre A e B. Portanto, podemos ter quatro situações: A e B podem ter alguns elementos em comum, A e B podem ser totalmente distintos, A pode conter B ou B pode conter A. Assim, se para algum destes casos a sentença for falsa, o item estará incorreto.
Iniciamos analisando o caso em que A e B tenham alguns elementos em comum, como podemos ver na ilustração.
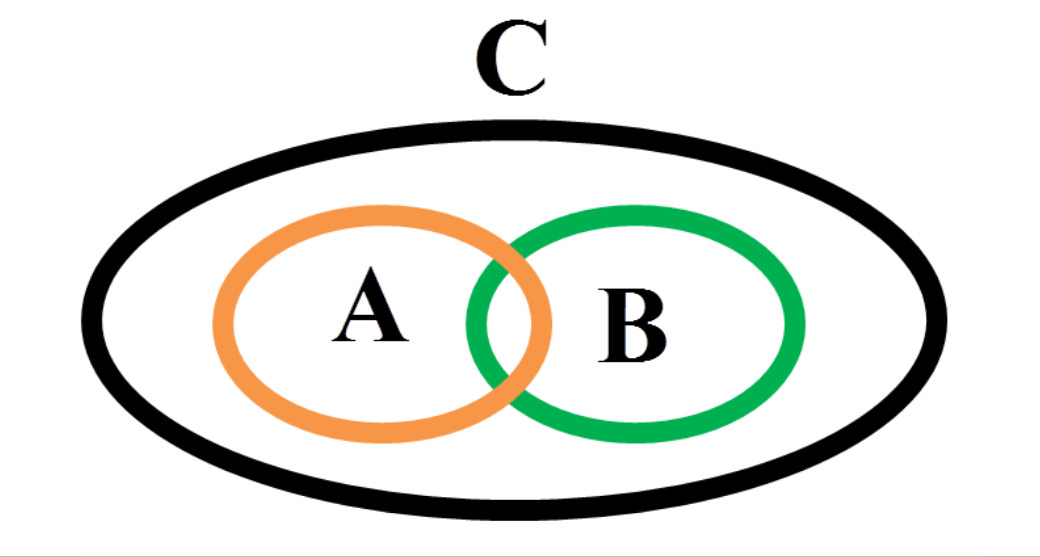
Em seguida, construiremos o conjunto (C\A) ∩ (A ∪ B) parte por parte, para finalmente compararmos com o conjunto C ∩ B . Primeiramente, temos (C\A) que significa os elementos que pertencem a C e não pertencem a A, representado por: (C-A).

Já (A ∪ B) significa os elementos que pertencem a A mais os que pertencem a B, porém sem repetir elementos iguais.

Assim, temos que (C\A) ∩ (A ∪ B) significa os elementos comuns ( que interseccionam) do conjunto (C\A) e do conjunto (A ∪ B), ou seja, os elementos que pertencem aos dois conjuntos. Logo, temos:

A interseção C ∩ B significa os elementos que pertencem aos dois conjuntos C e B, ou seja, o próprio conjunto B, visto que B pertence a C.

Portanto, observando os dois conjuntos (C\A) ∩ (A ∪ B) e C ∩ B percebemos que são diferentes (C\A) ∩ (A ∪ B) ≠ C ∩ B. Portanto, o item está Errado.
Uma última dica, lembre que tínhamos quatro possíveis relações entre A e B. Como uma delas já verificamos ser falsa, a sentença é falsa. Entretanto, se tivéssemos escolhido a relação A e B podem ser totalmente distintos, a sentença (C\A) ∩ (A ∪ B) = C ∩ B é verdadeira. Assim, deveríamos analisar as outros relações, onde constataríamos a falsidade do item.
Ademais, acompanhe outros exercícios de raciocínio lógico clicando aqui ou tabela verdade aqui. Ou melhor ainda, adquira nosso Treinamento Completo de Raciocínio Lógico com 145 páginas de questões resolvidas e comentadas das principais bancas de concurso do Brasil (Cespe, FCC, ESAF).