A meia-vida de determinado medicamento – função exponencial
Neste post abordaremos as funções que descrevem a meia-vida de determinado medicamento. Estas funções são do tipo exponencial. A temática deste post é baseada na questão enviado por um dos nossos alunos. Esta questão é do vestibular da UFRGS de 2020.
(UFRGS 2020) A concentração de alguns medicamentos no organismo está relacionada com a meia-vida, ou seja, o tempo necessário para que a quantidade inicial do medicamento no organismo seja reduzida pela metade. Considere que a meia-vida de um determinado medicamento é de 6 horas. Sabendo que um paciente ingeriu 120mg desse medicamento às 10 horas, assinale a alternativa que representa a melhor aproximação para a concentração desse medicamento, no organismo desse paciente, às 16 horas do dia seguinte.
(A) 2,75 mg.
(B) 3 mg.
(C) 3,75 mg.
(D) 4 mg.
(E) 4,25 mg.
Resolução:
Primeiramente, se você estiver em um vestibular, você pode/deve resolver da forma mais rápida possível para sobrar tempo para as demais questões. Assim, vou apresentar duas formas de resolver: uma a que julgo mais rápida/intuitiva e outra utilizando conhecimentos de funções exponenciais.
Primeira forma:
A primeira é a forma mais rápida. A questão diz que a meia-vida é de 6 horas, ou seja, a cada 6 horas o medicamento no organismo reduz pela metade. Portanto, basta fazer uma tabela em que na linha superior a cada coluna você soma 6 horas e na linha inferior você divide pela metade (por 2).
| Primeiro dia | Segundo dia | ||||
| 10h | 16h | 22h | 04h | 10h | 16h |
| 120mg | 60mg | 30mg | 15mg | 7,5mg | 3,75mg |
Portanto, a resposta é a letra C.
Segunda forma:
A segunda forma de resolver é utilizando os conhecimentos de funções exponenciais. A função exponencial geral de meia-vida é da seguinte forma
onde t é a variável tempo decorrido, 
é a quantidade inicial e c é a constante de decaimento. A quantidade inicial a questão já nos informa que é 120mg, assim, temos
.
A segunda informação dada pela questão é que a meia-vida é de 6 horas. Assim, a quantidade inicial cai para 60mg em 6 horas. Substituindo estas informações na função temos
.
Agora iremos fazer uma série de manipulações para determinarmos a constante c,
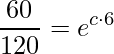
Em seguida, aplicamos o logaritmo natural em ambos os lados
.
Mas por que aplicar o logaritmo natural? Pois queremos manipular a equação a fim de isolar a variável c, para isto iremos utilizar a Propriedade da Potência dos logaritmos. Assim, aplicando está propriedade temos
e como 
temos
.
Portanto,
.
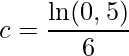Dessa forma, substituindo c na função desejada temos
[latex size=”25″]\displaystyle =120\cdot e^{ln(0,5)\cdot\frac{t}{6}}[/latex]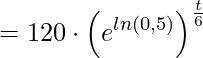
.
Por fim, como 
, temos que
.
Finalmente, aplicando o tempo desejado na função obtida, obteremos o resultado. São 14 horas do primeiro dia mais 16 horas do segundo dia, assim, se passaram 30 horas que o paciente ingeriu o medicamento. Portanto, temos
[latex size=”25″]\displaystyle =120\cdot \left(0,5\right)^{5}=3,75[/latex].
Portanto, a resposta correta é a letra C.
